题目内容
已知全集U=R,A={x|x≤a+2},B={x|x≥a2},若∁U(A∩B)=R,则a的取值范围是( )
| A、[-1,2] |
| B、(-1,2) |
| C、(-∞,-1]∪[2,+∞) |
| D、(-∞,-1)∪(2,+∞) |
考点:交、并、补集的混合运算
专题:集合
分析:根据A与B交集的补集为R,得到A与B的交集为空集,列出关于a的不等式,求出不等式的解集即可确定出a的范围.
解答:
解:∵全集U=R,A={x|x≤a+2},B={x|x≥a2},且∁U(A∩B)=R,
∴A∩B=∅,即a+2<a2,即a2-a-2>0,
分解因式得:(a-2)(a+1)>0,
解得:a<-1或a>2,
则a的范围是(-∞,-1)∪(2,+∞),
故选:D.
∴A∩B=∅,即a+2<a2,即a2-a-2>0,
分解因式得:(a-2)(a+1)>0,
解得:a<-1或a>2,
则a的范围是(-∞,-1)∪(2,+∞),
故选:D.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
已知x1,x2是方程(x-1)2=-1的两相异根,当x1=1-i(i为虚数单位)时,则x22为( )
| A、-2i | B、1+i |
| C、2i | D、1-i |
已知等比数列{an}的公比q<0,其前n 项的和为Sn,则a9S8与a8S9 的大小关系是( )
| A、a9S8>a8S9 |
| B、a9S8<a8S9 |
| C、a9S8≥a8S9 |
| D、a9S8≤a8S9 |
函数f(x)在定义域R上不是常函数,且f(x)满足条件,对任何x∈R,都有f(x+2)=f(2-x),f(1+x)=-f(x),则f(x)是( )
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、既奇又偶函数 |
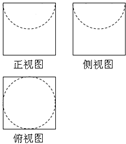 如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是
如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是 如图,在直三棱柱ABC-A1B1C1,中,AC=BC=
如图,在直三棱柱ABC-A1B1C1,中,AC=BC=