题目内容
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC中点,点E为BC边上的动点,且
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC中点,点E为BC边上的动点,且| BE |
| EC |
(1)求证:平面ADE⊥平面PBC;
(2)是否存在实数λ,使得二面角P-DE-B的余弦值为
| 2 |
| 3 |
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)取PB中点N,连结MN、AN,由已知得四边形ADMN为平行四边形,由AP⊥AD,AB⊥AD,得AD⊥平面PAB,从而AN⊥MN,由AP=AB,得AN⊥PB,由此能证明平面ADM⊥平面PBC.
(2)以A为原点,AB方向为x轴,AD方向为y轴,AP方向为z轴,建立空间直角坐标系A-xyz,求出平面PDE的法向量和平面DEB的法向量,利用向量法能求出λ=3或λ=
.
(2)以A为原点,AB方向为x轴,AD方向为y轴,AP方向为z轴,建立空间直角坐标系A-xyz,求出平面PDE的法向量和平面DEB的法向量,利用向量法能求出λ=3或λ=
| 1 |
| 3 |
解答:
(本小题满分12分)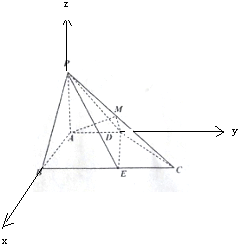
解:(1)取PB中点N,连结MN、AN,
∵M是PC中点,∴MN∥BC,MN=
BC=2,
又∵BC∥AD,∴MN∥AD,MN=AD,
∴四边形ADMN为平行四边形,
∵AP⊥AD,AB⊥AD,∴AD⊥平面PAB,
∴AD⊥AN,∴AN⊥MN,∵AP=AB,∴AN⊥PB,
∴AN⊥平面PBC,
∵AN?平面ADM,∴平面ADM⊥平面PBC.(6分)
(2)存在符合条件的λ.
以A为原点,AB方向为x轴,AD方向为y轴,AP方向为z轴,
建立空间直角坐标系A-xyz,
设E(2,t,0),P(0,0,2),D(0,2,0),B(2,0,0)
从而
=(0,2,-2),
=(2,t-2,0),
则平面PDE的法向量为
=(2-t,2,2),
又平面DEB即为xAy平面,其法向量
=(0,0,1),
则cos<
,
>=
=
=
,
解得t=3或t=1,进而λ=3或λ=
.(12分)

解:(1)取PB中点N,连结MN、AN,
∵M是PC中点,∴MN∥BC,MN=
| 1 |
| 2 |
又∵BC∥AD,∴MN∥AD,MN=AD,
∴四边形ADMN为平行四边形,
∵AP⊥AD,AB⊥AD,∴AD⊥平面PAB,
∴AD⊥AN,∴AN⊥MN,∵AP=AB,∴AN⊥PB,
∴AN⊥平面PBC,
∵AN?平面ADM,∴平面ADM⊥平面PBC.(6分)
(2)存在符合条件的λ.
以A为原点,AB方向为x轴,AD方向为y轴,AP方向为z轴,
建立空间直角坐标系A-xyz,
设E(2,t,0),P(0,0,2),D(0,2,0),B(2,0,0)
从而
| PD |
| DE |
则平面PDE的法向量为
| n1 |
又平面DEB即为xAy平面,其法向量
| n2 |
则cos<
| n1 |
| n2 |
| ||||
|
|
| 2 | ||
|
| 2 |
| 3 |
解得t=3或t=1,进而λ=3或λ=
| 1 |
| 3 |
点评:本小题主要考查立体几何的相关知识,具体涉及到线面以及面面的垂直关系、二面角的求法及空间向量在立体几何中的应用.本小题对考生的空间想象能力与运算求解能力有较高要求.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
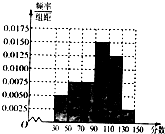 从某校高一期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图,如图所示.根据频率分布直方图,估计该次数学考试的平均分为( )
从某校高一期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图,如图所示.根据频率分布直方图,估计该次数学考试的平均分为( )| A、46 | B、82 | C、92 | D、102 |
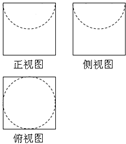 如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是
如图是一个无盖器皿的三视图,正视图、侧视图和俯视图 中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是 如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.
如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF. 为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),己知测试平均成绩在区间[30,60)有20人.
为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),己知测试平均成绩在区间[30,60)有20人.