题目内容
已知函数y=f(x)和y=g(x)的图象关于y轴对称,且f(x)=2x2+4x-2.
(Ⅰ)求函数y=g(x)的解析式;
(Ⅱ)当k<
时,解不等式
<
.
(Ⅰ)求函数y=g(x)的解析式;
(Ⅱ)当k<
| 1 |
| 2 |
| 4 |
| f(x)+g(x) |
| k |
| x-1 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)设y=g(x)图象上任意一点P(x,y),根据函数y=f(x)和y=g(x)的图象关于y轴对称,则求出P关于y轴的对称点P′,代入f((x)即可得函数y=g(x)的解析式;
(Ⅱ)将不等式“移项,通分”,然后化简等价转化为(x-1)(x+1)(k(x+1)-1)>0,根据k的正负和根的大小进行分类讨论,分别求解不等式,即可得到但.
(Ⅱ)将不等式“移项,通分”,然后化简等价转化为(x-1)(x+1)(k(x+1)-1)>0,根据k的正负和根的大小进行分类讨论,分别求解不等式,即可得到但.
解答:
解:(Ⅰ)设函数y=g(x)图象上任意一点P(x,y),
∴点P(x,y)关于y轴对称点为P′(-x,y),
∵函数y=f(x)和y=g(x)的图象关于y轴对称,
∴P′(-x,y)一定在函数y=f(x)图象上,
又∵f(x)=2x2+4x-2,
则代入y=2x2+4x-2,可得y=2x2-4x-2,
故函数y=g(x)的解析式为g(x)=2x2-4x-2;
(Ⅱ)由(Ⅰ)可知,f(x)=2x2+4x-2,g(x)=2x2-4x-2,
∴不等式
<
整理可得,不等式即为
<0,
即等价于(x-1)(x+1)(k(x+1)-1)>0,
①当k=0时,不等式即为(x-1)2<0,解得x∈(-1,1);
②当0<k<
时,不等式即为(x-1)(x+1)(x+1-
)>0,解得x∈(-1,1)∪(
-1,+∞);
③当k<0时,不等式即为(x+1)(x-1)(x+1-
)<0,解得x∈(-1,1)∪(-∞,
-1).
综合①②③,可得当k=0时,解集为(-1,1),
当0<k<
时,解集为x∈(-1,1)∪(
-1,+∞),
当k<0时,解集为x∈(-1,1)∪(-∞,
-1).
∴点P(x,y)关于y轴对称点为P′(-x,y),
∵函数y=f(x)和y=g(x)的图象关于y轴对称,
∴P′(-x,y)一定在函数y=f(x)图象上,
又∵f(x)=2x2+4x-2,
则代入y=2x2+4x-2,可得y=2x2-4x-2,
故函数y=g(x)的解析式为g(x)=2x2-4x-2;
(Ⅱ)由(Ⅰ)可知,f(x)=2x2+4x-2,g(x)=2x2-4x-2,
∴不等式
| 4 |
| f(x)+g(x) |
| k |
| x-1 |
| 1-k(x+1) |
| x2-1 |
即等价于(x-1)(x+1)(k(x+1)-1)>0,
①当k=0时,不等式即为(x-1)2<0,解得x∈(-1,1);
②当0<k<
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| k |
③当k<0时,不等式即为(x+1)(x-1)(x+1-
| 1 |
| k |
| 1 |
| k |
综合①②③,可得当k=0时,解集为(-1,1),
当0<k<
| 1 |
| 2 |
| 1 |
| k |
当k<0时,解集为x∈(-1,1)∪(-∞,
| 1 |
| k |
点评:本题考查了函数解析式的求解,分式不等式的解法,高次不等式的解法.本题解题的关键是如何进行合理的分类讨论.对于分式不等式,一般是“移项,通分”,将分式不等式转化为各个因式的正负问题.高次不等式一般选用“穿根法”进行求解,“穿根法”要注意先确定各因式的根,在数轴上按照从小到大标出来,确定各因式的系数为正值,根据“奇穿偶不穿”的原则,即可得到不等式的解集.属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
定义在R上的偶函数f(x)满足f(x)=-
且f(4)=-2,则f(2018)的值为( )
| 1 |
| f(x+3) |
| A、4 | ||
| B、-2 | ||
| C、2 | ||
D、
|
在空间直角坐标系中,点P(-2,4,4)关于x轴和坐标原点的对称点分别为P1和P2,则|P1P2|=( )
| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
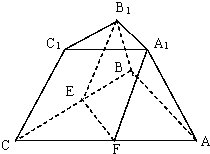 在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.
在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.