Question

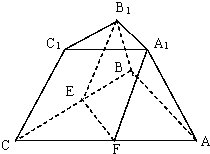在上、下底面对应边之比为1：2的正三棱台中，过上底面一边A₁B₁作一个平行于棱的平面A₁B₁ EF，求这个平面分三棱台所成的两部分体积之比．

Answer 1

考点：组合几何体的面积、体积问题

专题：计算题

分析：由题意可证六面体CEF-C₁B₁A₁是三棱柱，设棱台的上底面面积为S，高为h，求出三棱柱的体积，用间接法求出另一部分的体积，再求比值．

解答： 解：∵CC₁∥平面A₁B₁ EF，∴AA₁∥BB₁∥CC₁，
∴△CEF与△C₁B₁A₁全等，
∴六面体CEF-C₁B₁A₁是三棱柱，设棱台的上底面面积为S，高为h，
则V_棱柱=Sh，
∵上、下底面对应边之比为1：2，
∴棱台的下底面面积为4S，
∴V_棱台=

1

3

（S+

S×4S

+4S）h=

7

3

Sh，
∴两部分体积之比为

Sh

7 3 Sh-Sh

=

3

4

．

点评：本题考查了棱柱的体积计算，棱台的体积计算．