题目内容
已知非负实数x,y满足
,若实数k满足y+1=k(x+1),则( )
|
A、k的最小值为1,k的最大值为
| ||||
B、k的最小值为
| ||||
C、k的最小值为
| ||||
D、k的最小值为
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,y+1=k(x+1)过定点(-1,-1),利用数形结合以及直线斜率的意义进行求解即可.
解答:
 解:y+1=k(x+1)过定点(-1,-1),
解:y+1=k(x+1)过定点(-1,-1),
作出不等式组对应的平面区域如图:
则由图象知MC的斜率最小,MA的斜率最大,
其中A(0,4),C(1,0),
则MA的斜率k=
=5,
MC的斜率k=
=
,
故k的最小值为
,k的最大值为5,
故选:C
 解:y+1=k(x+1)过定点(-1,-1),
解:y+1=k(x+1)过定点(-1,-1),作出不等式组对应的平面区域如图:
则由图象知MC的斜率最小,MA的斜率最大,
其中A(0,4),C(1,0),
则MA的斜率k=
| -1-4 |
| -1-0 |
MC的斜率k=
| -1-0 |
| -1-1 |
| 1 |
| 2 |
故k的最小值为
| 1 |
| 2 |
故选:C
点评:本题主要考查线性规划的应用,利用直线斜率的公式结合数形结合是解决本题的关键.

练习册系列答案
相关题目
若(1-x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a1 十a2 十a3十a4十a5的值等于( )
| A、-31 | B、0 | C、1 | D、32 |
甲乙两名同学参加某项技能比赛,7名裁判给两人打出的分数如下茎叶图所示,依此判断( )

| A、甲成绩稳定且平均成绩较高 |
| B、乙成绩稳定且平均成绩较高 |
| C、甲成绩稳定,乙平均成绩较高 |
| D、乙成绩稳定,甲平均成绩较高 |
已知函数f(x)是定义在R上的偶函数,且对任意的实数x1≠x2(x1>0,x2>0)时,有
>0成立,如果实数t满足f(lnt)-f(1)≤f(1)-f(ln
),那么t的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| 1 |
| t |
| A、(0,e] | ||
B、[0,
| ||
| C、[1,e] | ||
D、[
|
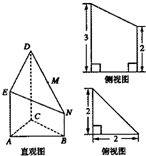 如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.