题目内容
若(1-x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a1 十a2 十a3十a4十a5的值等于( )
| A、-31 | B、0 | C、1 | D、32 |
考点:二项式系数的性质
专题:计算题,二项式定理
分析:根据题意,在(1-x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5中,令x=-1可得a0=32,令x=0可得a0+a1+a2+a3+a4+a5=1,两式综合可得答案.
解答:
解:在(1-x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,
令x=-1可得,25=a0,则a0=32,
令x=0可得,(1-0)5=1=a0+a1+a2+a3+a4+a5,则a0+a1+a2+a3+a4+a5=1,
则a1+a2+a3+a4+a5=(a0+a1+a2+a3+a4+a5)-a0=1-32=-31;
故选:A.
令x=-1可得,25=a0,则a0=32,
令x=0可得,(1-0)5=1=a0+a1+a2+a3+a4+a5,则a0+a1+a2+a3+a4+a5=1,
则a1+a2+a3+a4+a5=(a0+a1+a2+a3+a4+a5)-a0=1-32=-31;
故选:A.
点评:本题考查二项式定理的运用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入.

练习册系列答案
相关题目
依据三角函数线,做出如下四个判断:①sin
=sin
;②cos
=cos(-
);③tan
>tan
;④sin
>sin
,其中判断正确的有( )
| π |
| 6 |
| 7π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| 3π |
| 8 |
| 3π |
| 5 |
| 4π |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知非负实数x,y满足
,若实数k满足y+1=k(x+1),则( )
|
A、k的最小值为1,k的最大值为
| ||||
B、k的最小值为
| ||||
C、k的最小值为
| ||||
D、k的最小值为
|
执行右边的程序框图,则输出的A是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
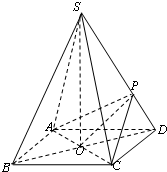 四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的
四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的
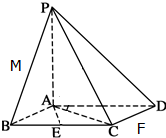 如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.
如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.