题目内容
设数列{an}的前n项和为Sn,满足(1-q)Sn+qan=1,且q(q-1)≠0.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若S3,S9,S6成等差数列,求证:a2,a8,a5成等差数列.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若S3,S9,S6成等差数列,求证:a2,a8,a5成等差数列.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(Ⅰ)求出a1=1.利用当n≥2时,由Sn-Sn-1=an,利用q(q-1)≠0,说明{an}是以1为首项,q为公比的等比数列,求出通项公式.
(Ⅱ)求出Sn=
,灵活S3+S6=2S9,得到a2+a5=2a8.说明a2,a8,a5成等差数列.
(Ⅱ)求出Sn=
| 1-anq |
| 1-q |
解答:
解:(Ⅰ)当n=1时,由(1-q)S1+qa1=1,a1=1.
当n≥2时,由(1-q)Sn+qan=1,得(1-q)Sn-1+qan-1=1,两式相减得an=qan-1,
又q(q-1)≠0,所以{an}是以1为首项,q为公比的等比数列,
故an=qn-1.
(Ⅱ)由(Ⅰ)可知Sn=
,又S3+S6=2S9,得
+
=
,
化简得a3+a6=2a9,两边同除以q得a2+a5=2a8.
故a2,a8,a5成等差数列.
当n≥2时,由(1-q)Sn+qan=1,得(1-q)Sn-1+qan-1=1,两式相减得an=qan-1,
又q(q-1)≠0,所以{an}是以1为首项,q为公比的等比数列,
故an=qn-1.
(Ⅱ)由(Ⅰ)可知Sn=
| 1-anq |
| 1-q |
| 1-a3q |
| 1-q |
| 1-a6q |
| 1-q |
| 2(1-a9q) |
| 1-q |
化简得a3+a6=2a9,两边同除以q得a2+a5=2a8.
故a2,a8,a5成等差数列.
点评:本题考查等差数列以及等比数列的综合应用,数列求和以及通项公式的求法,考查分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知非负实数x,y满足
,若实数k满足y+1=k(x+1),则( )
|
A、k的最小值为1,k的最大值为
| ||||
B、k的最小值为
| ||||
C、k的最小值为
| ||||
D、k的最小值为
|
执行右边的程序框图,则输出的A是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
的定义域为( )
| lg(1-2x) |
| A、(-∞,0] | ||
| B、(-∞,0) | ||
C、(0,
| ||
D、(-∞,
|
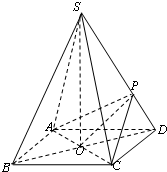 四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的
四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的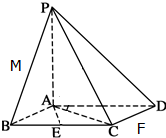 如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.
如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.