题目内容
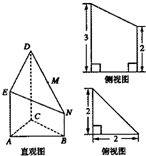 如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)在答题纸上的虚线框内画出该几何体的正视图,并标上数据;
(2)求证:EM∥平面ABC;
(3)试问在边BC上是否存在点G,使GN⊥平面NED.若存在,确定点G的位置;若不存在,请说明理由.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离,空间向量及应用
分析:(1)由题意画出正视图即可.
(2)证明FM
EA,可得四边形EAFM是平行四边形,即有AF∥EM,又AF⊆平面ABC,从而证明EM∥平面ABC.
(3)用向量法,建立空间坐标系,依据题设条件直接给出点的坐标,用向量表示出位置关系对应的方程,进行求解,若解出的坐标存在于所要求的位置,则说明存在.
(2)证明FM
| ∥ |
. |
(3)用向量法,建立空间坐标系,依据题设条件直接给出点的坐标,用向量表示出位置关系对应的方程,进行求解,若解出的坐标存在于所要求的位置,则说明存在.
解答:
 解:
解: (1)正视图如图所示.(注:不标中间实线扣1分)…(2分)
(1)正视图如图所示.(注:不标中间实线扣1分)…(2分)
(2)证明:俯视图和侧视图,得∠CAB=90°,
DC=3,CA=AB=2,EA=2,BN=1,EA⊥ABC,
EA∥DC∥NB.取BC的中点F,连接FM、EM,
则FM∥DC∥EA,且FM=
(BN+DC)=2.…(4分)
∴FM
EA,
∴四边形EAFM是平行四边形,
∴AF∥EM,又AF⊆平面ABC,
∴EM∥平面ABC.…(7分)
(3)以A为原点,CA为x轴,AB为y轴,AE为z轴建立如图所示的空间直角坐标系,
则有A(0,0,0),E(0,0,2),B(0,2,0),
D(-2,0,3),N(0,2,1),C(-2,0,0).
设
=(-2,-2,2),
=(0,-2,1),
=(2,2,0),
=(2,2,1).
假设在BC边上存在点G满足题意,
设
=λ
=(2λ,2λ,0),λ∈[0,1],
则
=
-
=(2,2,1)-(2λ,2λ,0)=(2-2λ,2-2λ,1),
∵GN⊥平面NED,
∴
,即
,
∴边BC上存在点D,满足CG=
CB时,GN⊥平面NED.…(12分)
 解:
解: (1)正视图如图所示.(注:不标中间实线扣1分)…(2分)
(1)正视图如图所示.(注:不标中间实线扣1分)…(2分)(2)证明:俯视图和侧视图,得∠CAB=90°,
DC=3,CA=AB=2,EA=2,BN=1,EA⊥ABC,
EA∥DC∥NB.取BC的中点F,连接FM、EM,
则FM∥DC∥EA,且FM=
| 1 |
| 2 |
∴FM
| ∥ |
. |
∴四边形EAFM是平行四边形,
∴AF∥EM,又AF⊆平面ABC,
∴EM∥平面ABC.…(7分)
(3)以A为原点,CA为x轴,AB为y轴,AE为z轴建立如图所示的空间直角坐标系,
则有A(0,0,0),E(0,0,2),B(0,2,0),
D(-2,0,3),N(0,2,1),C(-2,0,0).
设
| ND |
| NE |
| CB |
| CN |
假设在BC边上存在点G满足题意,
设
| CG |
| CB |
则
| GN |
| CN |
| CG |
∵GN⊥平面NED,
∴
|
|
∴边BC上存在点D,满足CG=
| 3 |
| 4 |
点评:本题是一个立体几何综合题,主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间向量的应用,涉及到的定理与技巧较多,对答题者的空间感知能力,问题的转化能力要求较高,考查了转化思想,属于中档题.

练习册系列答案
相关题目
设函数f(x)=|lnx|-
的两个零点为x1,x2,则有( )
| 1 |
| x+1 |
| A、x1x2<1 | ||
| B、x1x2=1 | ||
C、1<x1x2<
| ||
D、x1x2≥
|
已知A,B是以O为圆心的单位圆上的动点,且|
|=
,则
•
=( )
| AB |
| 2 |
| OB |
| AB |
| A、-1 | ||||
| B、1 | ||||
C、-
| ||||
D、
|
依据三角函数线,做出如下四个判断:①sin
=sin
;②cos
=cos(-
);③tan
>tan
;④sin
>sin
,其中判断正确的有( )
| π |
| 6 |
| 7π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| 3π |
| 8 |
| 3π |
| 5 |
| 4π |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知非负实数x,y满足
,若实数k满足y+1=k(x+1),则( )
|
A、k的最小值为1,k的最大值为
| ||||
B、k的最小值为
| ||||
C、k的最小值为
| ||||
D、k的最小值为
|
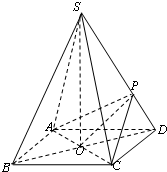 四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的
四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的