题目内容
设A，B是椭圆
+
=1的右顶点和上顶点，F1是它的左焦点，过F1作PF1⊥x轴，与椭圆在x轴上方的交点为P，OP∥AB．
（1）求椭圆的离心率；
（2）若AB=
，求该椭圆方程．
| x2 |
| a2 |
| y2 |
| b2 |
（1）求椭圆的离心率；
（2）若AB=
| 3 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（1）如图所示，由PF1⊥x轴，可得P(-c，
)．由于OP∥AB，可得kOP=kAB．再利用椭圆的离心率计算公式即可得出．
（2）由|AB|=
，可得
=
，与b=c=1，a2=b2+c2联立解出即可．
| b2 |
| a |
（2）由|AB|=
| 3 |
| a2+b2 |
| 3 |
解答：
解：（1）如图所示，
∵F1（-c，0），PF1⊥x轴，
∴P(-c，
)．
∵OP∥AB，∴kOP=kAB．
∴
=
，解得b=c．
∴a=
c．
∴椭圆的离心率e=
=
．
（2）∵|AB|=
，∴
=
，即a2+b2=3．
联立
，
解得b=c=1，a2=2．
∴椭圆的方程为：
+y2=1．
∵F1（-c，0），PF1⊥x轴，
∴P(-c，
| b2 |
| a |
∵OP∥AB，∴kOP=kAB．
∴
| ||
| -c |
| b |
| -a |
∴a=
| 2 |
∴椭圆的离心率e=
| c |
| a |
| ||
| 2 |
（2）∵|AB|=
| 3 |
| a2+b2 |
| 3 |
联立
|
解得b=c=1，a2=2．
∴椭圆的方程为：
| x2 |
| 2 |
点评：本题考查了椭圆的标准方程及其性质、平行线与斜率的关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
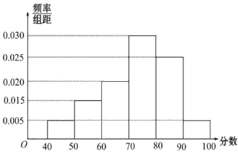某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
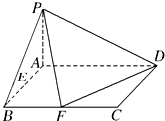已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E、F分别是线段AB、BC的中点．