题目内容
已知椭圆
+
=1的左右两个焦点分别为F1、F2,右顶点为A,上顶点为B,P为椭圆第一象限内一点.
(1)若S△PF1F2=S△PAF2,求椭圆的离心率;
(2)若S△PF1F2=S△PBF1,求直线PF1斜率.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若S△PF1F2=S△PAF2,求椭圆的离心率;
(2)若S△PF1F2=S△PBF1,求直线PF1斜率.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)根据S△PF1F2=S△PAF2,得
|F1F2||PF2|sin∠PF2F1=
|AF2||PF2|sin(180°-∠PF2F1),这样即可得到2c=a-c,所以便能求出离心率e=
;
(2)设直线PF1的斜率为k,可以写出PF1的方程,由已知条件知B到PF1的距离等于F2到PF1的距离,根据点到直线的距离公式,即可建立关于k的方程,解方程即可求出k.
| 1 |
| 2 |
| 1 |
| 2 |
| c |
| a |
(2)设直线PF1的斜率为k,可以写出PF1的方程,由已知条件知B到PF1的距离等于F2到PF1的距离,根据点到直线的距离公式,即可建立关于k的方程,解方程即可求出k.
解答:
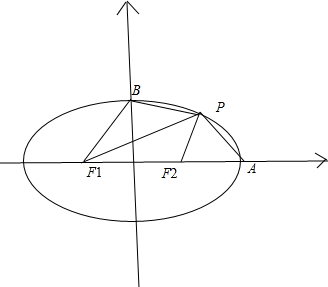 解:(1)如图,∵S△PF1F2=S△PAF2,
解:(1)如图,∵S△PF1F2=S△PAF2,
|F1F2||PF2|sin∠PF2F1═
|AF2||PF2|sin(180°-∠PF2F1);
∴|F1F2|=|AF2|,2c=a-c,3c=a,∴
=
,即椭圆的离心率为
.
(2)设PF1的斜率为k,F1(-c,0),则直线PF1的方程为:y=k(x+c),B(0,b),F2(c,0);
∵S△PF1F2=S△PBF1,点B到PF1的距离等于点F2到PF1的距离,即:
=
,∵P在第一象限,∴解得k=
=
;
即直线PF1的斜率为:
.
 解:(1)如图,∵S△PF1F2=S△PAF2,
解:(1)如图,∵S△PF1F2=S△PAF2,| 1 |
| 2 |
| 1 |
| 2 |
∴|F1F2|=|AF2|,2c=a-c,3c=a,∴
| c |
| a |
| 1 |
| 3 |
| 1 |
| 3 |
(2)设PF1的斜率为k,F1(-c,0),则直线PF1的方程为:y=k(x+c),B(0,b),F2(c,0);
∵S△PF1F2=S△PBF1,点B到PF1的距离等于点F2到PF1的距离,即:
| |-b+kc| | ||
|
| |2kc| | ||
|
| b |
| 3c |
| b | ||
3
|
即直线PF1的斜率为:
| b | ||
3
|
点评:考查椭圆的标准方程,椭圆的顶点及焦点,三角形面积公式,点到直线的距离公式.

练习册系列答案
相关题目
 一个几何体的三视图如图所示,其中主视图是边长为3cm的正方形,俯视图是半圆,求该几何体的表面积.
一个几何体的三视图如图所示,其中主视图是边长为3cm的正方形,俯视图是半圆,求该几何体的表面积.