题目内容
已知函数f(x)=x2,g(x)=(
)x-m,若对于?x1∈[-1,3],x2∈[0,2],使得f(x1)≥g(x2),求实数m的取值范围.
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:综合题,函数的性质及应用
分析:先利用函数的单调性求出f(x)∈[0,9],再利用x∈[0,2],g(x)≤0,即可求实数m的取值范围.
解答:
解:因为x∈[-1,3],所以f(x)∈[0,9],
又因为对?x1∈[-1,3],?x2∈[0,2],使得f(x1)≥g(x2)
所以x∈[0,2],g(x)≤0 ①,即(
)x-m≤0,所以m≥(
)x,
即x∈[0,2],m≥(
)x,则m≥(
)0,解得m≥1
又因为对?x1∈[-1,3],?x2∈[0,2],使得f(x1)≥g(x2)
所以x∈[0,2],g(x)≤0 ①,即(
| 1 |
| 2 |
| 1 |
| 2 |
即x∈[0,2],m≥(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查函数恒成立问题以及函数单调性的应用,考查计算能力和分析问题的能力,属于基本题.

练习册系列答案
相关题目
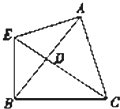 已知四边形ACBE,AB交CE于D点,BC=
已知四边形ACBE,AB交CE于D点,BC=