题目内容
17.已知函数f(x)=x2+2x+alnx(1)若曲线y=f(x)在x=1处切线的斜率为5,求实数a的值;
(2)当t≥1时,不等式f(2t-1)-2f(t)≥-3恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,计算f′(1)的值,求出a即可;
(2)由f(x)的解析式化简不等式,分离参数a,根据函数的单调性求出函数的最小值即可得到a的范围.
解答 解:(1)f′(x)=2x+2+$\frac{a}{x}$,
故f′(1)=4+a=5,解得:a=1;
(2)∵f(x)=x2+2x+alnx,
∴f(2t-1)≥2f(t)-3⇒2t2-4t+2≥2alnt-aln(2t-1)=aln $\frac{{t}^{2}}{2t-1}$.
当t≥1时,t2≥2t-1,∴ln $\frac{{t}^{2}}{2t-1}$≥0.即t>1时,a≤$\frac{{2(t-1)}^{2}}{ln\frac{{t}^{2}}{2t-1}}$恒成立.
又易证ln(1+x)≤x在x>-1上恒成立,
∴ln $\frac{{t}^{2}}{2t-1}$=ln[1+$\frac{{(t-1)}^{2}}{2t-1}$]≤$\frac{{(t-1)}^{2}}{2t-1}$<(t-1)2在t>1上恒成立,
当t=1时取等号,∴当t≥1时,ln $\frac{{t}^{2}}{2t-1}$≤(t-1)2,
∴由上知a≤2.故实数a的取值范围是(-∞,2].
点评 本题考查利用导数研究函数的单调性及函数恒成立时所取的条件.考查考生的运算、推导、判断能力.

练习册系列答案
相关题目
8.已知函数f(x)的部分图象如图,则f(x)的解析式可能为( )


| A. | f(x)=xsinx | B. | f(x)=xcosx-sinx | C. | f(x)=xcosx | D. | f(x)=xcosx+sinx |
12.在数列1,2,2,3,3,3,4,4,4,4,…中,第31项为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
2.已知角α的终边经过点P(4,-3),那么cosα-sinα的值是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{7}{5}$ | C. | $-\frac{1}{5}$ | D. | $\frac{7}{5}$ |
9.已知一几何体的三视图如图所示,则该几何体的体积为( )
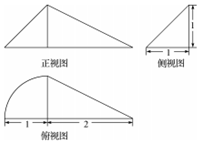

| A. | $\frac{π}{6}+\frac{1}{3}$ | B. | $\frac{π}{12}+1$ | C. | $\frac{π}{12}+\frac{1}{3}$ | D. | $\frac{π}{4}+\frac{1}{3}$ |
6.设x>0,由不等式x+$\frac{1}{x}$≥2,x+$\frac{4}{{x}^{2}}$≥3,x+$\frac{27}{{x}^{3}}$≥4,…,推广到x+$\frac{a}{{x}^{n}}$≥n+1,则a=( )
| A. | 2n | B. | 2n | C. | n2 | D. | nn |
7.下列命题中正确的是( )
| A. | 命题“?x0∈R,sinx0>1”的否定是“?x∈R,sinx>1” | |
| B. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” | |
| C. | 在△ABC中,A>B是sinA>sinB的充分不必要条件 | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |