题目内容

13．已知i是虚数单位，若z（1-2i）=2+4i，则复数z=$-\frac{6}{5}+\frac{8}{5}i$．．

分析 由z（1-2i）=2+4i，得$z=\frac{2+4i}{1-2i}$，然后利用复数代数形式的乘除运算化简复数z得答案．

解答 解：由z（1-2i）=2+4i，
得$z=\frac{2+4i}{1-2i}$=$\frac{（2+4i）（1+2i）}{（1-2i）（1+2i）}=\frac{-6+8i}{5}=-\frac{6}{5}+\frac{8}{5}i$，
故答案为：$-\frac{6}{5}+\frac{8}{5}i$．

点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案
相关题目
3．函数y=f（x）导函数f'（x）的图象如图所示，则下列说法正确的是（　　）
A．函数y=f（x）在（-∞，0）上单调递增B．函数y=f（x）的递减区间为（3，5）
C．函数y=f（x）在x=0处取得极大值D．函数y=f（x）在x=5处取得极小值
4．在等比数列{an}中，已知a7•a19=8，则a3•a23=（　　）
A．6B．7C．8D．9
1．已知椭圆C以原点为对称中心、右焦点为F（2，0），长轴长为4$\sqrt{2}$，直线l：y=kx+m（k≠0）交椭圆C于不同点两点A，B．
（1）求椭圆C的方程；
（2）是否存在实数k，使线段AB的垂直平分线经过点Q（0，3）？若存在求出k的取值范围；若不存在，请说明理由．
8．给出下列命题：
①函数y=sin（$\frac{5π}{2}$-2x）是偶函数；
②方程x=$\frac{π}{8}$是函数y=sin（2x+$\frac{5π}{4}$）的图象的一条对称轴方程；
③若α、β是第一象限角，且α＞β，则sinα＞sinβ；
④设x1、x2是关于x的方程|logax|=k（a＞0，a≠1，k＞0）的两根，则x1x2=1；
其中正确命题的序号是①②④．（填出所有正确命题的序号）
5．已知sin（α-β）=$\frac{3}{5}$，sin（α+β）=-$\frac{3}{5}$，且α-β∈（$\frac{π}{2}$，π），α+β∈（$\frac{3π}{2}$，2π），求cos2β的值．
12．已知函数f（x）=sin（2x+$\frac{π}{3}$），对任意的x1，x2，x3，且0≤x1＜x2＜x3≤π，都有|f（x1）-f（x2）|+|f（x2）-f（x3）|≤m成立，则实数m的最小值为3+$\frac{\sqrt{3}}{2}$．
9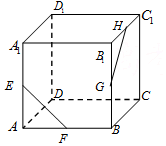．如图所示，在正方体ABCD-A1B1C1D1中，E，F，G，H分别为AA1，AB，BB1，B1C1的中点．则异面直线EF与GH所成的角等于（　　）
A．120°B．90°C．60°D．45°
10．过抛物线y=ax2（a＞0）的焦点F作一直线交抛物线于P，Q两点，若线段PF和线段FQ的长分别是p，q，则$\frac{1}{p}+\frac{1}{q}$等于（　　）
A．$\frac{1}{4a}$B．$\frac{1}{2a}$C．2aD．4a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网