题目内容

10．过抛物线y=ax2（a＞0）的焦点F作一直线交抛物线于P，Q两点，若线段PF和线段FQ的长分别是p，q，则$\frac{1}{p}+\frac{1}{q}$等于（　　）
A．$\frac{1}{4a}$B．$\frac{1}{2a}$C．2aD．4a

分析 选择题遵循一般结论利用特殊法，设PQ的斜率 k=0，因抛物线焦点坐标为（0，$\frac{1}{4a}$），把直线方程 y=$\frac{1}{4a}$ 代入抛物线方程得 x=±$\frac{1}{2a}$，可得 PF=FQ=$\frac{1}{2a}$，从而求得结果．

解答 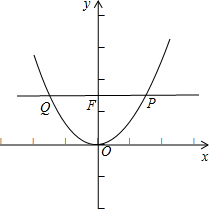解：不妨设PQ的斜率 k=0，因抛物线焦点坐标为（0，$\frac{1}{4a}$），
把直线方程 y=$\frac{1}{4a}$ 代入抛物线方程得 x=±$\frac{1}{2a}$，
∴PF=FQ=$\frac{1}{2a}$，即p=q=$\frac{1}{2a}$，则$\frac{1}{p}+\frac{1}{q}$=2a+2a=4a，
故选：D．

点评 本题考查抛物线的定义、标准方程，以及简单性质的应用，设k=0，求出PF=FQ=$\frac{1}{2a}$，是解题的关键，属于中档题．

练习册系列答案
相关题目
13．已知i是虚数单位，若z（1-2i）=2+4i，则复数z=$-\frac{6}{5}+\frac{8}{5}i$．．
1．已知△ABC的三内角A，B，C，所对三边分别为a，b，c，sin（A-$\frac{π}{4}$）=$\frac{\sqrt{2}}{10}$，若△ABC的面积S=24，b=10，则a的值是（　　）
A．5B．6C．7D．8
18．（Ⅰ） 在圆x2+y2=4上任取一点P，过点P作x轴的垂线段，D为垂足，当P在圆上运动时，求线段PD的中点Q的轨迹方程；
（Ⅱ）记（Ⅰ）中的轨迹为曲线为C，斜率为k（k≠0）的直线l交曲线C于M（x1，y1），N（x2，y2）两点，记直线OM，ON的斜率分别为k1，k2，当3（k1+k2）=8k时，证明：直线l过定点．
5．已知直线L：y=x+m与抛物线y2=8x交于A、B两点（异于原点），
（1）若直线L过抛物线焦点，求线段|AB|的长度；
（2）若OA⊥OB，求m的值．
15．设0＜x＜1，a，b都为大于零的常数，则$\frac{{a}^{2}}{x}$+$\frac{{b}^{2}}{1-x}$的最小值为（　　）
A．（a-b）2B．（a+b）2C．a2b2D．a2
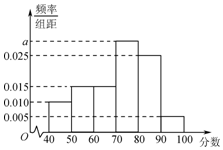2．某校从高一年级学生中随机抽取100名学生，将他们期中考试的数学成绩（均为整数）分成六段：[40，50），[50，60），…，[90，100]后得到频率分布直方图（如图所示），
（1）求分数在[70，80）中的人数；
（2）若用分层抽样的方法从分数在[40，50）和[50，60）的学生中共抽取5 人，该5 人中成绩在[40，50）的有几人；
（3）在（2）中抽取的5人中，随机抽取2 人，求分数在[40，50）和[50，60）各1 人的概率．
19．若α为第一象限角，且cosα=$\frac{2}{3}$，则tanα=$\frac{\sqrt{5}}{2}$．
20．已知集合A={x|m-1≤x≤2m+3}，函数f（x）=lg（-x2+2x+8）的定义域为B．
（1）当m=2时，求A∪B、（∁RA）∩B；
（2）若A∩B=A，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网