题目内容
1.已知椭圆C以原点为对称中心、右焦点为F(2,0),长轴长为4$\sqrt{2}$,直线l:y=kx+m(k≠0)交椭圆C于不同点两点A,B.(1)求椭圆C的方程;
(2)是否存在实数k,使线段AB的垂直平分线经过点Q(0,3)?若存在求出k的取值范围;若不存在,请说明理由.
分析 (1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)由题意$\left\{{\begin{array}{l}{2a=4\sqrt{2}}\\{c=2}\\{{b^2}={a^2}-{c^2}}\end{array}}\right.$,得a2,b2,
(2)假设存在斜率为k的直线,其垂直平分线经过点Q(0,3),
设A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),由$\left\{\begin{array}{l}\frac{x^2}{8}+\frac{y^2}{4}=1\\ y=kx+m\end{array}\right.$,得(1+2k2)x2+4mkx+2m2-8=0,△>0及kNQ•k=-1 进行判定.
解答 解:(1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),
由题意$\left\{{\begin{array}{l}{2a=4\sqrt{2}}\\{c=2}\\{{b^2}={a^2}-{c^2}}\end{array}}\right.$,得a2=8,b2=4,
所以椭圆C的方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$.…(5分)
(2)假设存在斜率为k的直线,其垂直平分线经过点Q(0,3),
设A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),
由$\left\{\begin{array}{l}\frac{x^2}{8}+\frac{y^2}{4}=1\\ y=kx+m\end{array}\right.$,得(1+2k2)x2+4mkx+2m2-8=0,…(6分)
△=16m2k2-4(1+2k2)(2m2-8)=64k2-8m2+32>0,所以8k2-m2+4>0,…(7分)
${x_1}+{x_2}=-\frac{4mk}{{1+2{k^2}}}$,∴${x_0}=\frac{{{x_1}+{x_2}}}{2}=-\frac{2mk}{{1+2{k^2}}}$,${y_0}=k{x_0}+m=\frac{m}{{1+2{k^2}}}$,…(8分)
∵线段AB的垂直平分线过点Q(0,3),∴kNQ•k=-1,即$\frac{{{y_0}-3}}{x_0}•k=-1$,∴-m=3+6k2,…(10分)
∵△>0,整理得36k4+28k2+5<0,显然矛盾∴不存在满足题意的k的值.…(12分)
点评 本题考查了直线与椭圆的位置关系、存在性问题、韦达定理、运算能力,属于中档题.

| A. | (x+2)2+y2=17 | B. | (x-2)2+y2=13 | C. | (x-1)2+y2=20 | D. | (x+1)2+y2=40 |
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | {1}∈{1,2,3} | B. | {1}?{1,2,3} | C. | {1}?{1,2,3} | D. | {1}={1,2,3} |
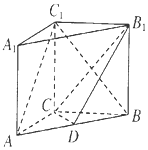 如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.