题目内容
9．
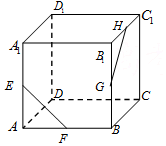如图所示，在正方体ABCD-A1B1C1D1中，E，F，G，H分别为AA1，AB，BB1，B1C1的中点．则异面直线EF与GH所成的角等于（ ）| A． | 120° | B． | 90° | C． | 60° | D． | 45° |
分析 如图所示，连接A1B，BC1，A1C1，则EF∥A1B，GH∥BC1，∠A1BC1是异面直线EF与GH所成的角，利用△A1BC1是等边三角形，即可得出结论．
解答 
解：如图所示，连接A1B，BC1，A1C1，则EF∥A1B，GH∥BC1，
∴∠A1BC1是异面直线EF与GH所成的角，
∵△A1BC1是等边三角形，
∴∠A1BC1=60°，
故选C．
点评 本题考查异面直线EF与GH所成的角，关键是作出异面直线EF与GH所成的角．
练习册系列答案
相关题目
12．已知圆C的圆心在x轴上，且经过A（5，2），B（-1，4）两点，则圆C的方程是（ ）
| A． | （x+2）2+y2=17 | B． | （x-2）2+y2=13 | C． | （x-1）2+y2=20 | D． | （x+1）2+y2=40 |
17．下列关系正确的是（ ）
| A． | {1}∈{1，2，3} | B． | {1}?{1，2，3} | C． | {1}?{1，2，3} | D． | {1}={1，2，3} |
4．对于函数f（x）=x图象上的任一点M，在函数g（x）=lnx上都存在点N（x0，y0），使以线段MN为直径的圆都经过坐标原点O，则x0必然在下面哪个区间内？（ ）
| A． | （$\frac{1}{{e}^{3}}$，$\frac{1}{{e}^{2}}$） | B． | （$\frac{1}{{e}^{2}}$，$\frac{1}{e}$） | C． | （$\frac{1}{e}$，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，1） |