题目内容
3.函数y=f(x)导函数f'(x)的图象如图所示,则下列说法正确的是( )
| A. | 函数y=f(x)在(-∞,0)上单调递增 | B. | 函数y=f(x)的递减区间为(3,5) | ||
| C. | 函数y=f(x)在x=0处取得极大值 | D. | 函数y=f(x)在x=5处取得极小值 |
分析 利用导数与函数单调性的关系以及函数在某点取得极值的条件即可判断.
解答 解:由函数y=f(x)导函数的图象可知:
当x<-1及3<x<5时,f′(x)<0,f(x)单调递减;
当-1<x<3及x>5时,f′(x)>0,f(x)单调递增.
所以f(x)的单调减区间为(-∞,-1),(3,5);单调增区间为(-1,3),(5,+∞),
f(x)在x=-1,5取得极小值,在x=3处取得极大值.
故选D.
点评 本题考查函数的单调性及极值问题,本题以图象形式给出导函数,由此研究函数有关性质,体现了数形结合思想.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
18.抛物线x2=4y的准线方程是( )
| A. | y=$\frac{1}{16}$ | B. | y=-$\frac{1}{16}$ | C. | y=x | D. | y=-1 |
15.设f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(2-x),(x<1)}\\{{2}^{x-1},(x≥1)}\end{array}\right.$,则f(-6)+f(log212)的值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
12.已知圆C的圆心在x轴上,且经过A(5,2),B(-1,4)两点,则圆C的方程是( )
| A. | (x+2)2+y2=17 | B. | (x-2)2+y2=13 | C. | (x-1)2+y2=20 | D. | (x+1)2+y2=40 |
 如图,椭圆E的左、右焦点分别为F1,F2,过F1且斜率为$\frac{4}{3}$的直线交椭圆E于P,Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为$\frac{1}{3}$或$\frac{5}{7}$.
如图,椭圆E的左、右焦点分别为F1,F2,过F1且斜率为$\frac{4}{3}$的直线交椭圆E于P,Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为$\frac{1}{3}$或$\frac{5}{7}$.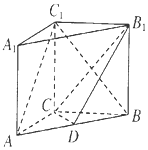 如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.