题目内容
函数f（x）的图象关于原点对称，g（x）=f（x）+3，且g（1）=5，则g（-1）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据奇函数图象的特征判断出函数是奇函数，利用奇函数的性质进行求值即可．
解答：
解：因为函数f（x）的图象关于原点对称，
所以函数f（x）是奇函数，则f（-x）=-f（x），
因为g（x）=f（x）+3，且g（1）=5，
所以g（1）=f（1）+3=5，解得f（1）=2，
则g（-1）=f（-1）+3=-f（1）+3=-2+3=1，
故答案为：1．
所以函数f（x）是奇函数，则f（-x）=-f（x），
因为g（x）=f（x）+3，且g（1）=5，
所以g（1）=f（1）+3=5，解得f（1）=2，
则g（-1）=f（-1）+3=-f（1）+3=-2+3=1，
故答案为：1．
点评：本题考查了偶函数、奇函数图象的特征，以及利用函数的奇偶性求函数值，属于基础题．
练习册系列答案
相关题目
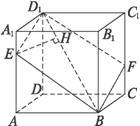如图，正方体ABCD-A1B1C1D1的棱长为a，过其对角线BD1的平面分别与AA1、CC1相交于点E，F，求截面四边形BED1F面积的最小值．