题目内容
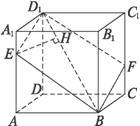 如图,正方体ABCD-A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值.
如图,正方体ABCD-A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值.考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:由条件根据面面平行的性质定理,证得四边形EBFD1的形状为平行四边形.作EH⊥BD1,H为垂足,且H∈BD1,要求四边形BED1F面积的最小值,转化为求EH的最小值. 由AA1∥平面BDD1B1,可得当且仅当EH为直线AA1到平面BDD1B1的距离时,EH最小为
,从而求得截面四边形BED1F面积的最小值2×(
BD1•EH)的值.
| ||
| 2 |
| 1 |
| 2 |
解答:
解:因为在长方体ABCD-A1B1C1D1中,平面AA1DD1与平面BB1C1CP平行,
而经过对角线BD1的平面分别与这两个相交于D1E与BF,
根据面面平行的性质定理,故D1E∥BF,同理可证BE∥FD1,
所以四边形EBFD1的形状为平行四边形.
作EH⊥BD1,H为垂足,且H∈BD1,要求四边形BED1F面积的最小值,转化为求EH的最小值.∵AA1∥平面BDD1B1,∴当且仅当EH为直线AA1到平面BDD1B1的距离时,EH最小,易得EHmin=
,
截面四边形BED1F面积的最小值为2×(
BD1•EH)=
a×
=
a.
而经过对角线BD1的平面分别与这两个相交于D1E与BF,
根据面面平行的性质定理,故D1E∥BF,同理可证BE∥FD1,
所以四边形EBFD1的形状为平行四边形.
作EH⊥BD1,H为垂足,且H∈BD1,要求四边形BED1F面积的最小值,转化为求EH的最小值.∵AA1∥平面BDD1B1,∴当且仅当EH为直线AA1到平面BDD1B1的距离时,EH最小,易得EHmin=
| ||
| 2 |
截面四边形BED1F面积的最小值为2×(
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查正方体的性质,面面平行的性质定理,体现了转化的数学思想,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知R为实数集,A={x|2x-3<3x},B={x|x≥2},则A∪B=( )
| A、{x|x≥2} |
| B、{x|x>-3} |
| C、{x|2≤x<3} |
| D、R |
已知不等式组
,则目标函数z=2x-y的最小值是( )
|
| A、8 | B、5 | C、4 | D、1+ln2 |
已知cos(
-φ)=
,且|φ|<
,则sin(2014π+φ)等于( )
| π |
| 2 |
| 1 |
| 3 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
 如图,在三棱柱ABC-A′B′C′中,点E、D分别是B′C′与BC的中点,求证:平面A′EB∥平面ADC′.
如图,在三棱柱ABC-A′B′C′中,点E、D分别是B′C′与BC的中点,求证:平面A′EB∥平面ADC′. 如图所示,AB为⊙O的直径,C为⊙O上一点,PA⊥平面ABC,AE⊥PB,垂足为E,AF⊥Pc,垂足为F,求证:PB⊥平面AEF.
如图所示,AB为⊙O的直径,C为⊙O上一点,PA⊥平面ABC,AE⊥PB,垂足为E,AF⊥Pc,垂足为F,求证:PB⊥平面AEF.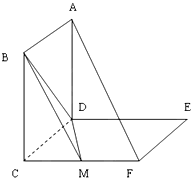 如图,正方形 ABCD 和正方形 CDEF所在平面互相垂直,M为FC的中点.
如图,正方形 ABCD 和正方形 CDEF所在平面互相垂直,M为FC的中点.