题目内容
4.已知向量$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(x,-1),若$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{b}$共线,则x的值等于( )| A. | -3 | B. | 1 | C. | 2 | D. | 1或2 |
分析 求出向量$\overrightarrow{a}$-$\overrightarrow{b}$,然后利用向量与$\overrightarrow{b}$共线,列出方程求解即可.
解答 解:$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(x,-1),
故$\overrightarrow{a}$$-\overrightarrow{b}$=(3-x,2)
若$\overrightarrow{a}$$-\overrightarrow{b}$与$\overrightarrow{b}$共线,
则2x=x-3,解得:x=-3,
故选:A.
点评 本题考查向量的共线以及向量的坐标运算,基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.定义在R上的奇函数f(x)在(-∞,0)上递增,f(2)=1,则满足|f(log${\;}_{\frac{1}{2}}$x)|>1的x的取值范围是( )
| A. | ($\frac{1}{4}$,4) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$)∪(2,+∞) | D. | (0,$\frac{1}{4}$)∪(4,+∞) |
19.已知$cos({\frac{π}{4}-α})=\frac{4}{5}$,则sin2α=( )
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $±\frac{24}{25}$ | D. | $±\frac{7}{25}$ |
9.已知中心在原点的双曲线,其右焦点与圆x2-4x+y2+1=0的圆心重合,且渐近线与该圆相离,则双曲线离心率的取值范围是( )
| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | (1,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | (2,+∞) |
16.在(1+x)+(1+x)2+(1+x)3+…+(1+x)11的展开式中,x2的系数是( )
| A. | 55 | B. | 66 | C. | 165 | D. | 220 |
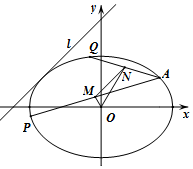 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.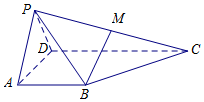 在四棱锥DN⊥平面PBC中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD=2,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥DN⊥平面PBC中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD=2,AB⊥AD,AB∥CD,点M是PC的中点.