题目内容
19.动点P,Q从点A(1,0)出发沿单位圆运动,点P按逆时针方向每秒钟转$\frac{π}{3}$弧度,点Q按顺时针方向每秒钟转$\frac{π}{6}$弧度,设P,Q第一次相遇时在点B,则B点的坐标为(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).分析 根据两个动点的角速度和第一次相遇时,两者走过的弧长和恰好是圆周长求出第一次相遇的时间,再由角速度和时间求出其中一点到达的位置,根据三角函数的定义得出此点的坐标.
解答 解:设P、Q第一次相遇时所用的时间是t,
则t•$\frac{π}{3}$+t•|-$\frac{π}{6}$|=2π,
∴t=4(秒),
即第一次相遇的时间为4秒;
设第一次相遇点为B,第一次相遇时P点已运动到终边在$\frac{π}{3}$•4=$\frac{4π}{3}$的位置,
则xB=-cos$\frac{π}{3}$•1=-$\frac{1}{2}$,
yB=-sin$\frac{π}{3}$•1=-$\frac{\sqrt{3}}{2}$.
∴B点的坐标为(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
故答案为:(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
点评 本题考查了圆周运动的角速度问题,认真分析题意列出方程,即第一次相遇时两个动点走过的弧长和是圆周,是解题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
9.已知函数f(x)=|x|(x-a)+1.当a=0时,函数f(x)的单调递增区间为(-∞,+∞);若函数g(x)=f(x)-a有3个不同的零点,则a的取值范围为(2$\sqrt{2}$-2,1) .
10.已知{an}是等比数列,则“a2<a4”是“{an}是单调递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.若sinα+$\sqrt{3}$cosα=2,则tan(π+α)=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
4.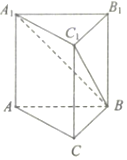 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )| A. | $\frac{8}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |