题目内容
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,M、N分别为棱BB1,B1C1的中点,由M,N,A三点确定的平面将该三棱柱分成体积不相等的两部分,则较小部分与较大部分的体积之比为 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:延长MN与CC1的交点为P,与CB的交点为Q,连结AP交A1C1为D,连结DN,得到截面为DNMA,由题意得A1D=2DC1,由此能求出较小部分与较大部分的体积之比.
解答:
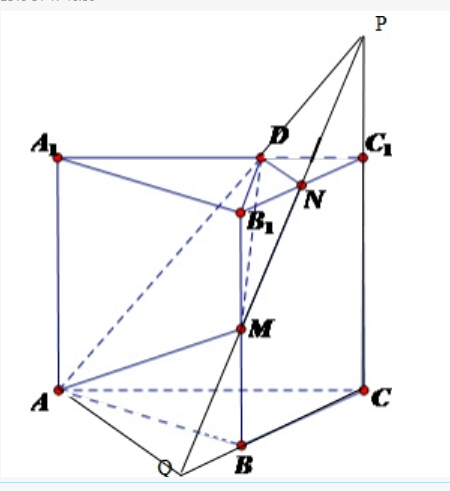 解:延长MN与CC1的交点为P,与CB的交点为Q,
解:延长MN与CC1的交点为P,与CB的交点为Q,
连结AP交A1C1为D,连结DN,
得到截面为DNMA,由题意得A1D=2DC1,
设三棱柱是直三棱柱,底面AB⊥BC,且设AB=BC=AA1=2,
∵QB=1,MB=1,NC=1,PC1=1,棱柱体积V=
×2×2×2=4,
∴下部分体积V下=VP-AQC-VP-DNC1-VM-AQB
=
×
×3×2×3-
×
×1×2-
×
×1×
×1
=
,
上部分体积V上=V-V下=4-
=
,
∴较小部分与较大部分的体积之比为:
=
=
.
故答案为:
.
 解:延长MN与CC1的交点为P,与CB的交点为Q,
解:延长MN与CC1的交点为P,与CB的交点为Q,连结AP交A1C1为D,连结DN,
得到截面为DNMA,由题意得A1D=2DC1,
设三棱柱是直三棱柱,底面AB⊥BC,且设AB=BC=AA1=2,
∵QB=1,MB=1,NC=1,PC1=1,棱柱体积V=
| 1 |
| 2 |
∴下部分体积V下=VP-AQC-VP-DNC1-VM-AQB
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
=
| 23 |
| 9 |
上部分体积V上=V-V下=4-
| 23 |
| 9 |
| 13 |
| 9 |
∴较小部分与较大部分的体积之比为:
| V上 |
| V下 |
| ||
|
| 13 |
| 23 |
故答案为:
| 13 |
| 23 |
点评:本题考查几何体中两部分体积之比的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知命题p:?m∈R,m+1≤0,命题q:?x∈R,x2+mx+1>0.若“p∧q”为假命题,则实数m的取值范围是( )
| A、(-∞,-2]∪(-1,+∞) |
| B、[2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,2] |
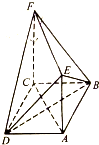 如图,在多面体ABCDEF中,底面ABCD是菱形,AE⊥平面ABCD,CF∥AE,AB=AC=AE=2,EF⊥平面BDE.
如图,在多面体ABCDEF中,底面ABCD是菱形,AE⊥平面ABCD,CF∥AE,AB=AC=AE=2,EF⊥平面BDE.