题目内容
已知2sinα+cosα=0 求
sin2α+
cos2α的值．
| 2 |
| 3 |
| 1 |
| 4 |
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：先求得tanα的值，从而可求cos2α的值，化简原式后代入即可求值．
解答：
解：∵由2sinα+cosα=0⇒cosα≠0且tanα=-
，
∴cos2α=
=
，
∴
sin2α+
cos2α=
+
=
．
| 1 |
| 2 |
∴cos2α=
| 1-tan2α |
| 1+tan2α |
| 3 |
| 5 |
∴
| 2 |
| 3 |
| 1 |
| 4 |
| 1-cos2α |
| 3 |
| 1+cos2α |
| 8 |
| 1 |
| 3 |
点评：本题主要考察了同角三角函数基本关系的运用，属于基本知识的考查．
练习册系列答案
相关题目
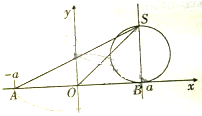平面内与两定点A（-a，0），B（a，0）（a＞0）的连线的斜率之积等于-