题目内容
已知命题p：?m∈R，m+1≤0，命题q：?x∈R，x2+mx+1＞0．若“p∧q”为假命题，则实数m的取值范围是（ ）
| A、（-∞，-2]∪（-1，+∞） |
| B、[2，+∞） |
| C、（-∞，-2]∪[2，+∞） |
| D、[-2，2] |
考点：复合命题的真假
专题：简易逻辑
分析：由P∧q 为假命题可知，由P∧q的否定为真，先求出P∧q为真的m的范围，进而可得答案．
解答：
解：由P∧q 为假命题可知，由P∧q 的否定为真，
因为命题p：?m∈R，m+1≤0，当m≤-1时是真命题，
当q为真时，由x2+mx+1＞0恒成立，可得-2＜m＜2，
若p∧q为真命题，必有-2＜m≤-1，
所以p∧q为假命题，则实数m的取值范围为：m≤-2或m＞-1，
综上知：m≤-2或m＞-1；
故选：A
因为命题p：?m∈R，m+1≤0，当m≤-1时是真命题，
当q为真时，由x2+mx+1＞0恒成立，可得-2＜m＜2，
若p∧q为真命题，必有-2＜m≤-1，
所以p∧q为假命题，则实数m的取值范围为：m≤-2或m＞-1，
综上知：m≤-2或m＞-1；
故选：A
点评：本题考查的知识点是复合命题的真假，解答过程中可能会有同学遗漏p与q同时为假的情况，在做题过程中要考虑全面．
练习册系列答案
相关题目
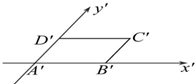如图所示，为一个平面图形的直观图，则它的实际形状为（ ）| A、平行四边形 | B、矩形 |
| C、菱形 | D、梯形 |
阅读下面的算法程序：
s=1
i=1
WHILE i＜=10
s=i*s
i=i+1
WEND
PRINT s
END
上述程序的功能是（ ）
s=1
i=1
WHILE i＜=10
s=i*s
i=i+1
WEND
PRINT s
END
上述程序的功能是（ ）
| A、计算3×10的值 |
| B、计算1×2×3×…×9的值 |
| C、计算1×2×3×…×10的值 |
| D、计算1×2×3×…×11的值 |