题目内容
已知函数f（x）=
．
（1）求函数f（x）的定义域；
（2）判定函数f（x）的奇偶性，并给出证明；
（3）若f（2x）=-
，求（
）x+log28+log2
的值．
| 2x+1 |
| 2x-1 |
（1）求函数f（x）的定义域；
（2）判定函数f（x）的奇偶性，并给出证明；
（3）若f（2x）=-
| 17 |
| 15 |
| 2 |
| 4 | 2 |
考点：函数单调性的判断与证明,函数的定义域及其求法,对数的运算性质
专题：函数的性质及应用
分析：（1）分式函数，需要令分母不为零，解得x的取值范围即可；
（2）根据奇函数的定义进行判断；
（3）首先求解x的值，然后，求解给定的代数式的值．
（2）根据奇函数的定义进行判断；
（3）首先求解x的值，然后，求解给定的代数式的值．
解答：
解：（1）∵函数f（x）=
．
∴2x-1≠0，
∴x≠0，
∴该函数的定义域为（-∞，0）∪（0，+∞）．
（2）∵f(-x)=
=-
=-f（x）．
∴f（-x）=-f（x）
∴函数f（x）为奇函数．
（3）∵f（2x）=
=-
，
∴x=-2，
∴（
）x+log28+log2
=（
）-2+3log22+
log22
=
+3+
=
；
∴（
）x+log28+log2
的值为
．
| 2x+1 |
| 2x-1 |
∴2x-1≠0，
∴x≠0，
∴该函数的定义域为（-∞，0）∪（0，+∞）．
（2）∵f(-x)=
| 2-x+1 |
| 2-x-1 |
=-
| 2x+1 |
| 2x-1 |
∴f（-x）=-f（x）
∴函数f（x）为奇函数．
（3）∵f（2x）=
| 4x+1 |
| 4x-1 |
| 17 |
| 15 |
∴x=-2，
∴（
| 2 |
| 4 | 2 |
=（
| 2 |
| 1 |
| 4 |
=
| 1 |
| 2 |
| 1 |
| 4 |
=
| 15 |
| 4 |
∴（
| 2 |
| 4 | 2 |
| 15 |
| 4 |
点评：本题重点考查了函数的定义域、奇偶性、对数的运算性质等知识，属于中档题．
练习册系列答案
相关题目
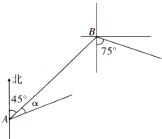在一次海上联合作战演习中，红方一艘侦察艇发现在北偏东45°方向，相距12n mile的水面上，有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进，若侦察艇以每小时14n mile的速度，沿北偏东45°+α方向拦截蓝方的小艇，若要在最短的时间内拦截住，求红方侦察艇所需的时间和角α的正弦值．（注：n mile是海里的英文符号）