题目内容
函数f（x）=2sinωx（ω＞0）在[-
，
]上递增，则ω的取值范围是 ．
| π |
| 6 |
| π |
| 4 |
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：根据正弦函数的单调性和周期之间的想即可得到结论．
解答：
解：若函数f（x）=2sinωx（ω＞0）在[-
，
]上递增，
则等价为在[-
，
]上递增，
∵过原点的函数f（x）的递增区间为[-
，
]，
则满足
≤
，
即T=
≥π，
则0＜ω≤2，
故答案为：（0，2]；
| π |
| 6 |
| π |
| 4 |
则等价为在[-
| π |
| 4 |
| π |
| 4 |
∵过原点的函数f（x）的递增区间为[-
| T |
| 4 |
| T |
| 4 |
则满足
| π |
| 4 |
| T |
| 4 |
即T=
| 2π |
| ω |
则0＜ω≤2，
故答案为：（0，2]；
点评：本题主要考查三角函数的单调性，本题巧妙地运用了正弦函数的单调性与周期之间的关系是解决本题的关键．
练习册系列答案
相关题目
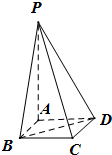如图所示，在四棱锥P-ABCD中，底面为正方形，PA⊥平面ABCD，且AB=2，AP=4，则点C到平面PBD的距离是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）满足：（1）对于任意的x1，x2∈R，有f（x1+x2）=f（x1）•f（x2）；（2）满足“对任意x1，x2∈R，且x1≠x2，都有
＜0”，下列函数满足这些条件的函数是（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、f（x）=lnx | ||
B、f（x）=x
| ||
| C、f（x）=ax（0＜a＜1） | ||
| D、f（x）=ax（a＞1） |
函数y=3cos（
x-
）的最小正周期是（ ）
| 2 |
| 5 |
| π |
| 6 |
| A、5π | ||
B、
| ||
| C、．2π | ||
D、
|