题目内容
直线l：
x-y-
=0，圆C：（x-3）2+y2=4，直线l与圆C交于A，B两点，则
•
等于（ ）
| 3 |
| 3 |
| AB |
| AC |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、2
|
考点：平面向量数量积的运算,直线与圆相交的性质
专题：计算题,平面向量及应用,直线与圆
分析：求出圆心到直线的距离，运用弦长公式a=2
，求出弦长，再运用向量的三角形法则，借助向量的数量积的定义，计算即可得到所求值．
| r2-d2 |
解答：
解：圆C：（x-3）2+y2=4的圆心为（3，0），半径为2，
则圆心C到直线l的距离d=
=
，
则截得的弦长|AB|=2
=2，
则有△ABC为等边三角形，
即有
•
=（
-
）•
=
2-
•
=4-4cos∠ACB=4-4cos60°=4-4×
=2．
故选A．
则圆心C到直线l的距离d=
|3
| ||||
|
| 3 |
则截得的弦长|AB|=2
| 4-3 |
则有△ABC为等边三角形，
即有
| AB |
| AC |
| CB |
| CA |
| AC |
| CA |
| CA |
| CB |
=4-4cos∠ACB=4-4cos60°=4-4×
| 1 |
| 2 |
故选A．
点评：本题考查直线和圆的位置关系，考查弦长公式的运用，考查平面向量的数量积的运用，考查运算能力，属于中档题．
练习册系列答案
相关题目
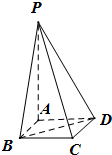如图所示，在四棱锥P-ABCD中，底面为正方形，PA⊥平面ABCD，且AB=2，AP=4，则点C到平面PBD的距离是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）满足：（1）对于任意的x1，x2∈R，有f（x1+x2）=f（x1）•f（x2）；（2）满足“对任意x1，x2∈R，且x1≠x2，都有
＜0”，下列函数满足这些条件的函数是（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、f（x）=lnx | ||
B、f（x）=x
| ||
| C、f（x）=ax（0＜a＜1） | ||
| D、f（x）=ax（a＞1） |