题目内容
设Sn，Tn分别是等差数列{an}，{bn}的前n项和，若
=
（n∈N*），则
=（ ）
| Sn |
| Tn |
| n |
| 2n+1 |
| a5 |
| b6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：等差数列的性质
专题：等差数列与等比数列
分析：根据等差数列的前n项和的特点和
=
，不妨设Sn=n2，Tn=n（2n+1），分别求出a5和b6，再求出
．
| Sn |
| Tn |
| n |
| 2n+1 |
| a5 |
| b6 |
解答：
解：由题意得，
=
，Sn、Tn分别是等差数列{an}，{bn}的前n项和，
所以不妨设Sn=n2，Tn=n（2n+1），
所以a5=S5-S4=25-16=9，b6=T6-T5=6×13-5×11=23，
则
=
，
故选：D．
| Sn |
| Tn |
| n |
| 2n+1 |
所以不妨设Sn=n2，Tn=n（2n+1），
所以a5=S5-S4=25-16=9，b6=T6-T5=6×13-5×11=23，
则
| a5 |
| b6 |
| 9 |
| 23 |
故选：D．
点评：本题考查等差数列的前n项和公式的灵活运用，以及数列的前n项和与数列中项的关系，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
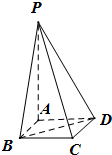如图所示，在四棱锥P-ABCD中，底面为正方形，PA⊥平面ABCD，且AB=2，AP=4，则点C到平面PBD的距离是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果函数y=f（x）在区间I上是增函数，而函数y=
在区间I上是减函数，那么称函数y=f（x）是区间I上“缓增函数”，区间I叫做“缓增区间”，若函数f（x）=
x2-x+
是区间I上“缓增函数”，则“缓增区间”I为（ ）
| f(x) |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| A、[1，+∞） | ||
B、[0，
| ||
| C、[0，1] | ||
D、[1，
|
已知定义在R上的连续函数f（x）是一个奇函数，则
[ex+f（x）]dx等于（ ）
| ∫ | 1 -1 |
A、e+
| ||
B、e-
| ||
| C、0 | ||
| D、无法计算 |
函数y=3cos（
x-
）的最小正周期是（ ）
| 2 |
| 5 |
| π |
| 6 |
| A、5π | ||
B、
| ||
| C、．2π | ||
D、
|
已知
+
是实数，其中i为虚数单位，则实数a等于（ ）
| a |
| 1+i |
| 1+i |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
D、-
|