题目内容
已知方程x2+xlog26+log23=0的两根为α，β，则(
)α•(
)β=（ ）
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
| B、36 | ||
| C、-6 | ||
| D、6 |
考点：函数的零点与方程根的关系,对数的运算性质
专题：函数的性质及应用
分析：利用韦达定理得到α+β，化简所求表达式，求解即可．
解答：
解：方程x2+xlog26+log23=0的两根为α，β，
所以α+β=-log26．
(
)α•(
)β=(
)α+β=(
)-log26=(2-2)-log26=36．
故选：B．
所以α+β=-log26．
(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故选：B．
点评：本题考查对数的运算法则的应用，函数的零点，考查计算能力．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则它的体积为（ ）
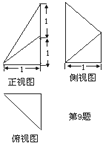
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
任取两个不同的1位正整数，它们的和是8的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
与向量
=（1，2，3），
=（3，1，2）都垂直的向量为（ ）
| a |
| b |
| A、（1，7，5） |
| B、（1，-7，5） |
| C、（-1，-7，5） |
| D、（1，-7，-5） |
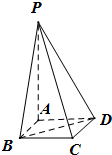如图所示，在四棱锥P-ABCD中，底面为正方形，PA⊥平面ABCD，且AB=2，AP=4，则点C到平面PBD的距离是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|