题目内容

执行如图所示的程序框图，输出的T=（　　）
A、29B、44C、52D、62
考点：循环结构
专题：算法和程序框图
分析：执行程序框图，依次写出每次循环得到的S，T，n的值，当S=12，n=4，T=29时，满足条件T＞2S，退出循环，输出T的值为29．
解答： 解：执行程序框图，有
S=3，n=1，T=2，
不满足条件T＞2S，S=6，n=2，T=8
不满足条件T＞2S，S=9，n=3，T=17
不满足条件T＞2S，S=12，n=4，T=29
满足条件T＞2S，退出循环，输出T的值为29．
故选：A．
点评：本题主要考察了程序框图和算法，属于基本知识的考查．
练习册系列答案
相关题目
与向量
a
=（1，2，3），
b
=（3，1，2）都垂直的向量为（　　）
A、（1，7，5）
B、（1，-7，5）
C、（-1，-7，5）
D、（1，-7，-5）
若方程ax2-2x+a=0的一根在区间（0，1）上，另一根在区间（1，2）上，则实数a的范围
 
．
函数f（x）=
x-
1
x
，x＜0
-2+lnx，x＞0
的零点个数是（　　）
A、0B、1C、2D、3
已知△ABC的外接圆的圆心为O，满足
CO
=m
CA
+n
CB
，4m+3n=2且|CB|=6，|CA|=4
3
，则
CA
•
CB
=
 
．
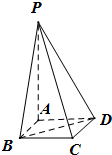如图所示，在四棱锥P-ABCD中，底面为正方形，PA⊥平面ABCD，且AB=2，AP=4，则点C到平面PBD的距离是（　　）
A、
2
3
B、
6
3
C、
4
3
D、
4
10
5
下列说法错误的个数是（　　）
①若数列{an}的通项为{an}=
1
n(n+1)
，则它的前100项和S100=
99
100

②若数列{an}的前n项和为Sn，若a1=1，且当n≥2时，恒有Sn=2an，则{an}是等比数列．
③如果定义在R上的偶函数f（x）有零点，则它的所有零点之和等于0．
④把函数y=sin（2x+
π
6
）的图象向右平移
π
4
个长度单位，即可得到y=sin（2x-
π
3
）的图象．
A、0B、1C、2D、3
已知f（x）=ax3+bsin x+3且f（1）=2014，f（-1）的值为
 
．
如果函数y=f（x）在区间I上是增函数，而函数y=
f(x)
x
在区间I上是减函数，那么称函数y=f（x）是区间I上“缓增函数”，区间I叫做“缓增区间”，若函数f（x）=
1
2
x2-x+
3
2
是区间I上“缓增函数”，则“缓增区间”I为（　　）
A、[1，+∞）
B、[0，
3
]
C、[0，1]
D、[1，
3
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网