题目内容

已知正方形ABCD，AB=2，若将△ABD沿正方形的对角线BD所在的直线进行翻折，则在翻折的过程中，四面体A-BCD的体积的最大值是
 
．
考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：当平面ABD垂直于平面BCD时，该三棱锥高为OA最大，通过计算可求得三棱锥的最大体积．
解答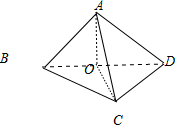： 解：三棱锥A-BCD的底面为△BCD，面积为2，易知当平面ABD垂直于平面BCD时，该三棱锥高为OA最大，体积为
1
3
•2•
2
=
2
2
3
．
故答案为：
2
2
3
．
点评：本题是基础题，考查折叠问题，体积的最值，确定当平面ABD垂直于平面BCD时，该三棱锥高为OA最大是关键．
练习册系列答案
相关题目
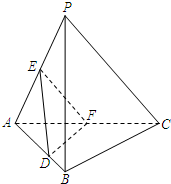如图，在三棱锥P-ABC中，平面PAC⊥平面ABC，∠BAC=60°，E，F分别是AP，AC的中点，点D在棱AB上，且AD=AC．求证：
（1）EF∥平面PBC；
（2）平面DEF⊥平面PAC．
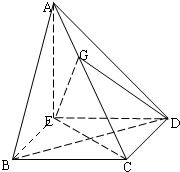如图，在四棱锥A-BCDE中，AE⊥平面BCDE，∠ABC=∠BCD=∠CDA=90°，AC=6
3
，BC=CD=6．
（Ⅰ）求证：BD⊥平面ACE；
（Ⅱ）设点G在棱AC上，且CG=2GA，试求三棱锥E-GCD的体积．
若函数f（x）=
x
ax+b
（a≠0），f（2）=1，又方程f（x）=x有唯一解，且a1=1，an+1=f（an），Sn=a1a2+a2a3+…+an-1•an，如果存在正整数M，使得对一切正整数n，Sn≤M都成立，则M的最小值为
 
．
在极坐标系中，点（2，
π
6
）到极轴的距离
 
．
在平面直角坐标系xOy中，已知双曲线
x2
9
-
y2
m
=1的一个焦点为（5，0），则实数m=
 
．
小明在做一道数学题目时发现：若复数z1=cosα1+isinα1，z2=cosα2+isinα2，z3=cosα3+isinα3（其中α1，α2，α3∈R），则z1•z2=cos（α1+α2）+isin（α1+α2），z2•z3=cos（α2+α3）+isin（α2+α3），根据上面的结论，可以提出猜想：z1•z2•z3=
 
．
在△ABC中，cos2
A
2
=
b+c
2c
（a，b，c分别为角A，B，C的对边），则cos
A+B
2
=
 
．
若变量x，y满足约束条件
x-y+2≥0
x-5y+10≤0
x+y-8≤0
，则z=3x-4y的取值范围是（　　）
A、[-11，3]
B、[-11，-3]
C、[-3，11]
D、[3，11]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网