题目内容
若变量x,y满足约束条件
,则z=3x-4y的取值范围是( )
|
| A、[-11,3] |
| B、[-11,-3] |
| C、[-3,11] |
| D、[3,11] |
考点:简单线性规划
专题:不等式的解法及应用
分析:画出不等式组表示可行域,要求线性目标函数的最值,就是直线(目标函数)截距的范围,求解即可.
解答:
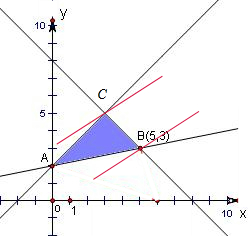 解:不等式组
解:不等式组
表示的区域如图,
其中A(0,2),B(5,3).C(3,5)
z=3x-4y的几何意义是
直线在y轴上的截距,当直线经过点B(5,3)时,z=15-12=3,取最大值为3,
当取得点C(3,5)时,z=3-20=-11,z取最小值为-11,
所以目标函数z=3x-4y的取值范围为[-11,3],
故选:A.
 解:不等式组
解:不等式组
|
其中A(0,2),B(5,3).C(3,5)
z=3x-4y的几何意义是
直线在y轴上的截距,当直线经过点B(5,3)时,z=15-12=3,取最大值为3,
当取得点C(3,5)时,z=3-20=-11,z取最小值为-11,
所以目标函数z=3x-4y的取值范围为[-11,3],
故选:A.
点评:本题利用直线斜率的几何意义,画出可行域是解题的关键.本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知f(x)=
,若函数g(x)=f(x)-kx+k只有一个零点,则k的取值范围是( )
|
| A、(-∞,-1)∪(1,+∞) |
| B、(-1,1) |
| C、[0,1] |
| D、(-∞,-1]∪[0,1] |
一个棱锥的三视图如图,则该棱锥的表面积为( )


A、48+12
| ||
B、48+24
| ||
C、72+12
| ||
D、72+24
|
已知a>0,设p:存在a∈R,使y=ax是R上的单调递减函数; q:存在a∈R,使函数g(x)=lg(2ax2+2x+1)的值域为R,如果“p∧q”为假,“p∨q”为真,则a的取值范围是( )
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(0,
|
直线l1:x+y-2
=0与直线l2:
(t为参数)的交点到原点O的距离是( )
| 2 |
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
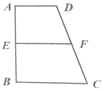 如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:
如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论: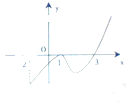 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: