题目内容
19．如图是一空间几何体的三视图，尺寸如图（单位：cm）．则该几何体的表面积是18+2$\sqrt{3}$cm2．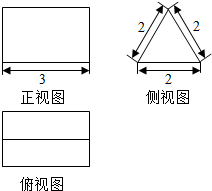
分析 由已知中的三视图可得：该几何体是一个以侧视图为底面的三棱柱，根据柱体表面积公式，可得答案．
解答 解：由已知中的三视图可得：该几何体是一个以侧视图为底面的三棱柱，
其底面是边长为2的正三角形，面积为：$\frac{\sqrt{3}}{4}×{2}^{2}$=$\sqrt{3}$，
底面周长为6，高为3，故侧面积为：18，
故几何体的表面积为：18+2$\sqrt{3}$，
故答案为：18+2$\sqrt{3}$
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
相关题目
9．复数$\frac{2-i}{1-i}$的共轭复数是（ ）
| A． | $\frac{3+i}{2}$ | B． | $\frac{1-i}{2}$ | C． | $\frac{3-i}{2}$ | D． | $\frac{-3-i}{2}$ |
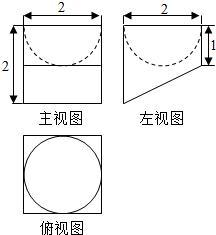
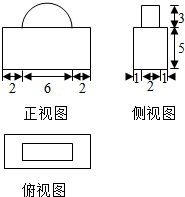将一个长、宽、高分别为10、4、8的长方体毛坯加工成某工件，如图为加工后该工件的三视图，则该工件的材料利用率（材料利用率=$\frac{新工件的体积}{毛坯的体积}$）是$\frac{200+9π}{320}$．
11．直线3x+4y+2m=0与圆x2+（y-$\frac{1}{2}$）2=1相切，且实数m的值为（ ）
| A． | log23 | B． | 2 | C． | log25 | D． | 3 |
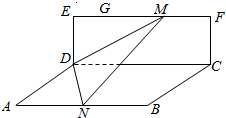如图，矩形CDEF所在的平面与矩ABCD所在的平面垂直，AD=$\sqrt{2}$，DE=$\sqrt{3}$，AB=4，$\overrightarrow{EG}$=$\frac{1}{4}$$\overrightarrow{EF}$，点M在线段GF上（包括两端点），点N在线段AB上，且$\overrightarrow{GM}$=$\overrightarrow{AN}$，则二面角M-DN-B的平面角的取值范围为[$\frac{π}{4}$，$\frac{π}{3}$]．