题目内容
9.已知:x=x1,x=x2是函数f(x)=$\frac{1}{3}$ax3-$\frac{1}{2}$ax2-x的两个极值点,且A(x1,$\frac{1}{{x}_{1}}$),B(x2,$\frac{1}{{x}_{2}}$),则直线AB与椭圆$\frac{{x}^{2}}{2}$+y2=1的位置关系为( )| A. | 相切 | B. | 相交 | C. | 相离 | D. | 位置关系不正确 |
分析 求出原函数的导函数,由函数f(x)=$\frac{1}{3}$ax3-$\frac{1}{2}$ax2-x有两个极值点,可得${x}_{1}+{x}_{2}=1,{x}_{1}{x}_{2}=-\frac{1}{a}$,把过A,B的直线方程整理为y=a(x-1),可知直线y=a(x-1)过定点(1,0),由此可知直线AB与椭圆$\frac{{x}^{2}}{2}$+y2=1的位置关系.
解答 解:由f(x)=$\frac{1}{3}$ax3-$\frac{1}{2}$ax2-x,得f′(x)=ax2-ax-1,
又函数f(x)=$\frac{1}{3}$ax3-$\frac{1}{2}$ax2-x有两个极值点,
∴方程ax2-ax-1=0有两个不等的实数根,
则a2+4a>0,且${x}_{1}+{x}_{2}=1,{x}_{1}{x}_{2}=-\frac{1}{a}$,
∴${k}_{AB}=\frac{\frac{1}{{x}_{2}}-\frac{1}{{x}_{1}}}{{x}_{2}-{x}_{1}}=-\frac{1}{{x}_{1}{x}_{2}}=a$,
则过AB的直线方程为y-$\frac{1}{{x}_{1}}=a(x-{x}_{1})$,
整理得:$y=ax+\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,
即y=a(x-1),
则直线y=a(x-1)过定点(1,0),
∴直线AB与椭圆$\frac{{x}^{2}}{2}$+y2=1的位置关系为相交.
故选:B.
点评 本题考查利用导数求函数的极值,考查了椭圆的简单性质,考查数学转化思想方法,是中档题.

练习册系列答案
相关题目
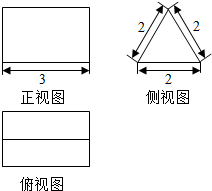
20. 如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
 如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )
如图是一个几何体的三视图,正视图是一个等腰直角三角形,侧视图为一个直角三角形,俯视图是一个直角梯形,则此几何体的表面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5+\sqrt{3}}{2}$ | D. | $\frac{5+\sqrt{3}}{2}$+$\sqrt{2}$ |
17.已知某几何体的三视图如图,其中主视图中半圆的直径为2,则该几何体的表面积为( )

| A. | 46 | B. | 52-π | C. | 52+3π | D. | 46+2π |
14.某地区2007年至2013年居民人均纯收入y(单位:千元)的数据如表:
(1)设y关于t的线性回归方程为y=bt+a,求b,a的值;
(2)利用(1)中的回归方程,预测该地区2016年居民人均纯收入.
(参考公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,a=$\overline{y}$-b$\overline{t}$)
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)利用(1)中的回归方程,预测该地区2016年居民人均纯收入.
(参考公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,a=$\overline{y}$-b$\overline{t}$)
18.函数f(x)=lnx-x2+4x+5的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |