题目内容
14.解方程:(1)32-x=2;
(2)3x+1=21-2x;
(3)($\frac{4}{9}$)x•($\frac{27}{8}$)x-1=$\frac{2}{3}$.
分析 (1)32-x=2,化为指数式2-x=log32,解得x即可得出;
(2)3x+1=21-2x,两边取对数可得:(x+1)lg3=(1-2x)lg2,解得x即可.
(3)($\frac{4}{9}$)x•($\frac{27}{8}$)x-1=$\frac{2}{3}$,化为$(\frac{2}{3})^{2x+3(1-x)}$=$\frac{2}{3}$,利用指数函数的单调性即可得出.
解答 解:(1)32-x=2,∴2-x=log32,解得x=2-log32;
(2)3x+1=21-2x,∴(x+1)lg3=(1-2x)lg2,解得x=$\frac{lg2-lg3}{lg3+2lg2}$.
(3)($\frac{4}{9}$)x•($\frac{27}{8}$)x-1=$\frac{2}{3}$,化为$(\frac{2}{3})^{2x+3(1-x)}$=$\frac{2}{3}$,∴-x+3=1,解得x=2.
点评 本题考查了指数函数与对数的单调性、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.若实数数列:1,a1,a2,a3,81成等比数列,则圆锥曲线${x^2}+\frac{y^2}{a_2}=1$的离心率是( )
| A. | $\sqrt{10}$ 或$\frac{{2\sqrt{2}}}{3}$ | B. | $\sqrt{10}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$或$\sqrt{10}$ |
6.下列各组空间向量相互垂直的是( )
| A. | $\overrightarrow{a}$=(0,1,-2),$\overrightarrow{b}$=(2,0,-1) | B. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-1,0,3) | ||
| C. | $\overrightarrow{a}$=(0,-1,-2),$\overrightarrow{b}$=(0,-2,4) | D. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-3,1,-1) |
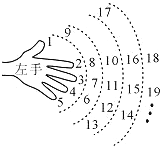 如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).
如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).