题目内容
11．直线3x+4y+2m=0与圆x2+（y-$\frac{1}{2}$）2=1相切，且实数m的值为（ ）| A． | log23 | B． | 2 | C． | log25 | D． | 3 |
分析 根据直线与圆相切，圆心到直线的距离d=r，列出方程求出m的值．
解答 解：因为直线3x+4y+2m=0与圆x2+（y-$\frac{1}{2}$）2=1相切，
所以圆心到直线的距离为d=r；
即$\frac{|0+2{+2}^{m}|}{\sqrt{{3}^{2}{+4}^{2}}}$=1，
化简得2+2m=5，
即2m=3，
解得m=log23．
故选：A．
点评 本题考查了直线与圆相切时圆心到直线的距离d=r的应用问题，是基础题目．
练习册系列答案
相关题目
6．下列各组空间向量相互垂直的是（ ）
| A． | $\overrightarrow{a}$=（0，1，-2），$\overrightarrow{b}$=（2，0，-1） | B． | $\overrightarrow{a}$=（3，-1，1），$\overrightarrow{b}$=（-1，0，3） | ||
| C． | $\overrightarrow{a}$=（0，-1，-2），$\overrightarrow{b}$=（0，-2，4） | D． | $\overrightarrow{a}$=（3，-1，1），$\overrightarrow{b}$=（-3，1，-1） |
16．若椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上有n个不同的点P1，P2，P3，…，Pn，F是右焦点，{|PnF|}组成等差数列，且公差d＞$\frac{1}{100}$，则n的最大值是（ ）
| A． | 199 | B． | 200 | C． | 99 | D． | 100 |
20．
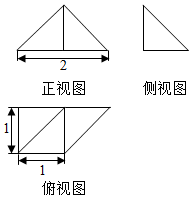如图是一个几何体的三视图，正视图是一个等腰直角三角形，侧视图为一个直角三角形，俯视图是一个直角梯形，则此几何体的表面积是（ ）
如图是一个几何体的三视图，正视图是一个等腰直角三角形，侧视图为一个直角三角形，俯视图是一个直角梯形，则此几何体的表面积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{5+\sqrt{3}}{2}$ | D． | $\frac{5+\sqrt{3}}{2}$+$\sqrt{2}$ |