题目内容
已知函数f(x)=
sin2x+
(sin2x-cos2x)+
;
(1)求函数f(x)的最小正周期;
(2)若存在t∈[
,
]满足[f(t)]2-2
f(t)-m=0,求实数m的取值范围;
(3)求证:任意的x1∈[-
,
],存在唯一的x2∈[-
,
],使f(x1)•f(x2)=1成立.
| ||
| 2 |
| 1 |
| 2 |
| 2 |
(1)求函数f(x)的最小正周期;
(2)若存在t∈[
| π |
| 12 |
| π |
| 3 |
| 2 |
(3)求证:任意的x1∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析:(1)首先利用三角函数的恒等变换把函数的关系式变形成正弦型函数,进一步求出函数的周期.
(2)利用正弦型函数的定义域求出函数的值域,进一步利用存在性问题求出函数中参数的取值范围.
(3)利用函数具备严格的单调性来进行证明.
(2)利用正弦型函数的定义域求出函数的值域,进一步利用存在性问题求出函数中参数的取值范围.
(3)利用函数具备严格的单调性来进行证明.
解答:
解:(1)函数f(x)=
sin2x+
(sin2x-cos2x)+
=
sin2x-
cos2x+
=sin(2x-
)+
,
所以函数的最小正周期为;T=π;
(2)由于t∈[
,
],
所以:2t-
∈[0,
],
设:F(x)=[f(t)]2-2
f(t)=(f(t)-
)2-2∈[-2,-1],
存在t∈[
,
]满足[f(t)]2-2
f(t)-m=0,
所以:m的取值范围为:m∈[-2,-1]
(3)对任意的x1∈[-
,
],存在唯一的x2∈[-
,
],使f(x1)•f(x2)=1成立,
当x1∈[-
,
]时,使f(x1)f(x2)=1成立.
当x1∈[-
,
]时,2x1-
∈[-
,
],
所以:f(x1)=sin(2x1-
)+
∈[
-1,
+1],
f(x2)=
=sin(2x2-
)+
∈[
-1,
+1].
则:sin(2x2-
)=
-
∈[-1,1],
设:
-
=a(a∈[-1,1]),
由sin(2x2-
)=a.
解得:2x2-
=2kπ+arcsina或2x2-
=2kπ+π-arcsina,
所以x2的解集为:{x2|x2=kπ+
arcsina+
或x2=kπ-
arcsina+
}(k∈Z).
由于-
≤
arcsina+
≤
,
所以:
≤-
arcsina+
≤
,
由于函数在此区间内有严格的单调性.
所以:存在唯一的x2∈[-
,
],使f(x1)•f(x2)=1成立.
| ||
| 2 |
| 1 |
| 2 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 2 |
=sin(2x-
| π |
| 6 |
| 2 |
所以函数的最小正周期为;T=π;
(2)由于t∈[
| π |
| 12 |
| π |
| 3 |
所以:2t-
| π |
| 6 |
| π |
| 2 |
设:F(x)=[f(t)]2-2
| 2 |
| 2 |
存在t∈[
| π |
| 12 |
| π |
| 3 |
| 2 |
所以:m的取值范围为:m∈[-2,-1]
(3)对任意的x1∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
当x1∈[-
| π |
| 6 |
| π |
| 3 |
当x1∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
所以:f(x1)=sin(2x1-
| π |
| 6 |
| 2 |
| 2 |
| 2 |
f(x2)=
| 1 |
| f(x1) |
| π |
| 6) |
| 2 |
| 2 |
| 2 |
则:sin(2x2-
| π |
| 6 |
| 1 |
| f(x1) |
| 2 |
设:
| 1 |
| f(x1) |
| 2 |
由sin(2x2-
| π |
| 6 |
解得:2x2-
| π |
| 6 |
| π |
| 6 |
所以x2的解集为:{x2|x2=kπ+
| 1 |
| 2 |
| π |
| 12 |
| 1 |
| 2 |
| 7π |
| 12 |
由于-
| π |
| 6 |
| 1 |
| 2 |
| 7π |
| 12 |
| π |
| 3 |
所以:
| π |
| 3 |
| 1 |
| 2 |
| 7π |
| 12 |
| 5π |
| 6 |
由于函数在此区间内有严格的单调性.
所以:存在唯一的x2∈[-
| π |
| 6 |
| π |
| 3 |
点评:本题考查的知识要点:三角函数的恒等变换,正弦型函数的周期,存在性问题的应用,利用函数的单调性正面函数的唯一解.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
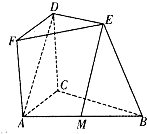 如图,四边形ACDF为正方形,且平面ACDF⊥平面BCDE,平面ACDF⊥平面ABC,BC=2DE,DE∥BC,M为AB的中点.
如图,四边形ACDF为正方形,且平面ACDF⊥平面BCDE,平面ACDF⊥平面ABC,BC=2DE,DE∥BC,M为AB的中点.
