题目内容
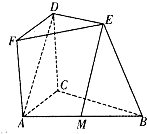 如图,四边形ACDF为正方形,且平面ACDF⊥平面BCDE,平面ACDF⊥平面ABC,BC=2DE,DE∥BC,M为AB的中点.
如图,四边形ACDF为正方形,且平面ACDF⊥平面BCDE,平面ACDF⊥平面ABC,BC=2DE,DE∥BC,M为AB的中点.(Ⅰ)证明:BC⊥AD;
(Ⅱ)证明EM∥平面ACDF.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)首先根据面面垂直,进一步转化成线面垂直,最后转化成线线垂直.
(Ⅱ)利用中点和三角形中位线,得到线线平行,最后转化成线面平行.
(Ⅱ)利用中点和三角形中位线,得到线线平行,最后转化成线面平行.
解答:
证明:(Ⅰ)四边形ACDF为正方形,且平面ACDF⊥平面BCDE,
所以:AC⊥CD,AC⊥平面CBDE
所以:AC⊥BC
又平面ACDF⊥平面ABC,
CD⊥AC
CD⊥平面ABC
CD⊥BC
所以:BC⊥平面ACDF
则:BC⊥AD
(Ⅱ)取AC的中点N,连接MN和DN,BC=2DE,DE∥BC,M为AB的中点.
所以:NM∥DE,MN=DE
所以:四边形MEDN是平行四边形.
则:ME∥DN
ME?平面ACDF
DN?平面ACDF
所以:EM∥平面ACDF
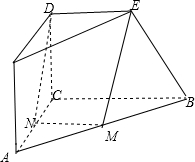
所以:AC⊥CD,AC⊥平面CBDE
所以:AC⊥BC
又平面ACDF⊥平面ABC,
CD⊥AC
CD⊥平面ABC
CD⊥BC
所以:BC⊥平面ACDF
则:BC⊥AD
(Ⅱ)取AC的中点N,连接MN和DN,BC=2DE,DE∥BC,M为AB的中点.
所以:NM∥DE,MN=DE
所以:四边形MEDN是平行四边形.
则:ME∥DN
ME?平面ACDF
DN?平面ACDF
所以:EM∥平面ACDF

点评:本题考查的知识要点:线面垂直面面垂直与线线垂直之间的相互转化,线面平行的判定定理得应用,三角形中位线定理的应用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
将5本不同的书摆成一排,若书甲与书乙必须相邻,而书丙与书丁不能相邻,则不同的摆法种数为( )
| A、48 | B、24 | C、20 | D、12 |
函数f(x)=lgx-1的零点是( )
| A、10 | ||
B、
| ||
| C、(10,0) | ||
| D、(0,10) |
已知数列{an}是等差数列,若a2+2,a4+4,a6+6构成等比数列,这数列{an}的公差d等于( )
| A、1 | B、-1 | C、2 | D、-2 |
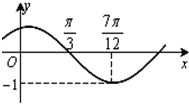 函数f(x)=sin(ωx+φ)(其中|φ|<
函数f(x)=sin(ωx+φ)(其中|φ|<| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|