题目内容

经过抛物线y=
1
4
x2的焦点作直线与抛物线交于A（x1，y1），B（x2，y2）两点，若y1+y2=5，则线段AB的长等于（　　）
A、5B、6C、7D、8
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由题意求出抛物线的焦点坐标和准线方程，根据抛物线的定义，证出|AB|=|AF|+|BF|=y1+y2+2，结合题中数据即可求出|AB|的值．
解答： 解：由题意得，抛物线的方程为：x2=4y，
则焦点坐标F（0，1），准线方程为y=-1，
由抛物线的定义得，|AF|=y1+1，且|BF|=y2+1
又y1+y2=5，
所以|AB|=|AF|+|BF|=y1+y2+2=7，
故选：C．
点评：本题考查了抛物线的标准方程，抛物线的定义：抛物线上的点到焦点的距离与到准线的距离相等，以及焦点弦公式的应用．
练习册系列答案
相关题目
焦点在y轴上，且焦点到准线的距离是2的抛物线的标准方程是（　　）
A、y2=8x或y2=-8x
B、x2=8y或x=-8y
C、y2=4x或y2=-4x
D、x2=4y或x2=-4y
y=sin（3x-
π
6
）的单调递减区间是（　　）
A、[
2kπ
3
+
4π
9
，
2kπ
3
+
5π
9
]（k∈Z）
B、[
2kπ
3
+
2π
9
，
2kπ
3
+
5π
3
]（k∈Z）
C、[
2kπ
3
+
2π
3
，
2kπ
3
+
5π
3
]（k∈Z）
D、[
2kπ
3
+
2π
9
，
2kπ
3
+
5π
9
]（k∈Z）
如图，Rt△ABC中，CD为斜边AB上的高，CD=6，且AD：BD=3：2，则斜边AB上的中线CE的长为（　　）
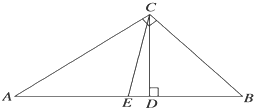
A、5
6
B、
5
6
2
C、
15
D、
3
10
2
已知数列{an}为等比数列，a4+a7=2，a5•a6=-8，则a1+a10的值为（　　）
A、7B、-5C、5D、-7
在极坐标系中，直线ρsin（θ+
π
4
）=2被圆ρ=4截得的弦长为（　　）
A、2
2
B、2
3
C、4
2
D、4
3
已知函数f（x）=x3+3mx2+nx+m2在x=-1时有极值为0，则m+n=（　　）
A、11B、4或11C、4D、8
下列参数方程与方程y=2x表示相同图象的是（　　）
A、
x=t2
y=2t2
B、
x=sinθ
y=2sinθ
C、
x=2t
y=t2
D、
x=tanθ
y=2tanθ
计算定积分
∫
π
6
π
12
cos2xdx的值是（　　）
A、
3
-1
4
B、
3
-1
2
C、
3
-1
D、2（
3
-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网