题目内容
已f(x)为偶函数且
f(x)dx=8,则
f(x)dx等于( )
| ∫ | 6 0 |
| ∫ | 6 -6 |
| A、0 | B、4 | C、8 | D、16 |
考点:定积分
专题:导数的概念及应用
分析:利用已知被积函数是偶函数,所以(-6,0)和(0,6)的积分相等,得到所求.
解答:
解:∵f(x)为偶函数,
∴
f(x)dx=2
f(x)dx=2×8=16,
故选:D.
∴
| ∫ | 6 -6 |
| ∫ | 6 0 |
故选:D.
点评:本题考查了偶函数的性质以及积分的意义;偶函数的对称区间的定积分相等,奇函数对称区间的定积分相反.

练习册系列答案
相关题目
已知关于某设备的使用年限x和所支出的维修费用y(万元)如右图所示,若由资料知y对x呈线性相关关系,且线性回归方程
=
x+
的回归系数
=1.2,估计使用10年时,维修费用是( )(参考公式:
=
-
x)
 |
| y |
 |
| b |
 |
| a |
| ? |
| b |
 |
| a |
 |
| y |
 |
| b |
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A、12.2 | B、12.3 |
| C、12.38 | D、12.4 |
下列各数中最小的数是( )
| A、111111(2) |
| B、150(6) |
| C、1000(4) |
| D、81(8) |
对于函数f(x)=asinx+bx3+c(a,b∈R,c∈Z)选取a,b,c的一组值计算f(2)和f(-2),所得出的正确结果一定不可能是( )
| A、1和3 | B、1和2 |
| C、2和4 | D、4和6 |
如图,Rt△ABC中,CD为斜边AB上的高,CD=6,且AD:BD=3:2,则斜边AB上的中线CE的长为( )
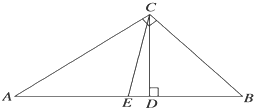

A、5
| ||||
B、
| ||||
C、
| ||||
D、
|
命题p:对?x∈R,都有x2-x+1>0成立,则p的否定形式为( )
| A、对?x∈R,都有x2-x+1≤0 |
| B、?x0∈R,都有x02-x0+1≤0 |
| C、?x0∈R,都有x02-x0+1>0 |
| D、对?x∈R,都有x2-x+1<0 |
在极坐标系中,直线ρsin(θ+
)=2被圆ρ=4截得的弦长为( )
| π |
| 4 |
A、2
| ||
B、2
| ||
C、4
| ||
D、4
|
在△ABC中,已知a=3,b=4,c=5,则角C为( )
| A、90° | B、60° |
| C、45° | D、30° |
下列函数在区间(0,+∞)上单调递减的是( )
| A、y=-x2+8x+9 | ||
| B、y=10x | ||
| C、y=cosx | ||
D、y=
|