题目内容
设
,
分别是x轴,y轴正方向上的单位向量,
=3cosθ
+3sinθ
,θ∈(0,
),
=-
.若用α来表示
与
的夹角,则α等于( )
| i |
| j |
| OP |
| i |
| j |
| π |
| 2 |
| OQ |
| i |
| OP |
| OQ |
| A、θ | ||
B、
| ||
C、
| ||
| D、π-θ |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:先运用坐标运算求得
•
,再由两个向量的数量积的定义,得到cosα=-cosθ,再由θ的范围及诱导公式求出α的值.
| OP |
| OQ |
解答:
解:
•
=(3cosθ
+3sinθ
)•(-
)=-3cosθ+0=-3cosθ.
由两个向量的数量积的定义可得
•
=3×1×cosα=3cosα,
∴3cosα=-3cosθ,cosα=-cosθ=cos(π-θ),
∵θ∈(0,
)
∴π-θ∈(
,π),
故有α=π-θ.
故选:D.
| OP |
| OQ |
| i |
| j |
| i |
由两个向量的数量积的定义可得
| OP |
| OQ |
∴3cosα=-3cosθ,cosα=-cosθ=cos(π-θ),
∵θ∈(0,
| π |
| 2 |
∴π-θ∈(
| π |
| 2 |
故有α=π-θ.
故选:D.
点评:本题主要考查两个向量的数量积的定义,诱导公式以及两个向量数量积公式的应用,两个向量垂直的性质,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
焦点在y轴上,且焦点到准线的距离是2的抛物线的标准方程是( )
| A、y2=8x或y2=-8x |
| B、x2=8y或x=-8y |
| C、y2=4x或y2=-4x |
| D、x2=4y或x2=-4y |
已知直线l:3x+4y-12=0与圆C:
(θ为参数)的位置关系是( )
|
| A、相切 | B、相离 |
| C、相交但直线不过圆心 | D、直线过圆心 |
若直线
(t为参数)与直线4x+ky=1垂直,则常数k=( )
|
| A、7 | B、5 | C、4 | D、6 |
下列各数中最小的数是( )
| A、111111(2) |
| B、150(6) |
| C、1000(4) |
| D、81(8) |
y=sin(3x-
)的单调递减区间是( )
| π |
| 6 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
如图,Rt△ABC中,CD为斜边AB上的高,CD=6,且AD:BD=3:2,则斜边AB上的中线CE的长为( )
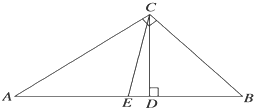

A、5
| ||||
B、
| ||||
C、
| ||||
D、
|
下列参数方程与方程y=2x表示相同图象的是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|