题目内容
函数y=|x+1|-2x零点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:函数的图象,根的存在性及根的个数判断
专题:函数的性质及应用
分析:由f(x)=|x+1|-2x=0得|x+1|-2x,分别作出函数y=|x+1|与y=2x的图象,利用数形结合求出函数f(x)的零点个数.
解答:
解:由f(x)=|x+1|-2x=0得|x+1|-2x,分别作出函数y=|x+1|与y=2x的图象如图:
由图象可知两个函数有3个交点,即函数y=|x+1|-2x的零点个数为3个,
故选:D.

由图象可知两个函数有3个交点,即函数y=|x+1|-2x的零点个数为3个,
故选:D.
点评:本题考查函数的图象,函数零点知识,考查函数与方程,数形结合的思想,准确画好图是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线l:3x+4y-12=0与圆C:
(θ为参数)的位置关系是( )
|
| A、相切 | B、相离 |
| C、相交但直线不过圆心 | D、直线过圆心 |
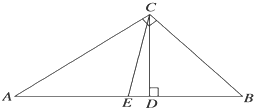
如图,Rt△ABC中,CD为斜边AB上的高,CD=6,且AD:BD=3:2,则斜边AB上的中线CE的长为( )

A、5
| ||||
B、
| ||||
C、
| ||||
D、
|
在极坐标系中,直线ρsin(θ+
)=2被圆ρ=4截得的弦长为( )
| π |
| 4 |
A、2
| ||
B、2
| ||
C、4
| ||
D、4
|
已知函数f(x)=x3+3mx2+nx+m2在x=-1时有极值为0,则m+n=( )
| A、11 | B、4或11 | C、4 | D、8 |
在△ABC中,已知a=3,b=4,c=5,则角C为( )
| A、90° | B、60° |
| C、45° | D、30° |
下列参数方程与方程y=2x表示相同图象的是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
在△ABC中,a、b、c分别是A、B、C的对边,面积S=a2-(b-c)2,则sinA=( )
A、
| ||
B、
| ||
C、
| ||
D、
|