题目内容
7.已知椭圆mx2+ny2=1(n>m>0)的离心率为$\frac{{\sqrt{2}}}{2}$,则双曲线mx2-ny2=1的离心率为( )| A. | 2 | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 通过椭圆的离心率推出mn的关系,然后求解双曲线的离心率即可.
解答 解:椭圆mx2+ny2=1(n>m>0)的离心率为$\frac{{\sqrt{2}}}{2}$,
可得:a2=$\frac{1}{m}$,b2=$\frac{1}{n}$,
$\frac{{c}^{2}}{{a}^{2}}=\frac{\frac{1}{m}-\frac{1}{n}}{\frac{1}{m}}$=$\frac{1}{2}$,
∴$\frac{m}{n}=\frac{1}{2}$.
双曲线mx2-ny2=1的离心率为:$\sqrt{\frac{\frac{1}{m}+\frac{1}{n}}{\frac{1}{m}}}$=$\sqrt{1+\frac{m}{n}}$=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$.
故选:B.
点评 本题考查椭圆的简单性质以及双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
18.用反证法证明命题“若a2+b2≠0,则a,b不全为0(a,b∈R)”时,其假设正确的是( )
| A. | a,b中至少有一个为0 | B. | a,b中至少有一个不为0 | ||
| C. | a,b全为0 | D. | a,b中只有一个不为0 |
15.若向量$\overrightarrow a=(3,2)$,$\overrightarrow b=(0,-1)$,则向量$\vec a+\vec b$的坐标是( )
| A. | (3,-1) | B. | (-3,1) | C. | (-3,-1) | D. | (3,1) |
16.若函数f(x)=x(x-c)2在x=3处有极大值,则c=( )
| A. | 9 | B. | 3 | C. | 3或9 | D. | 以上都不对 |
17.运行如图所示的程序框图,若输入的n=3,x=2,则输出的y的值为( )


| A. | 9 | B. | 18 | C. | 20 | D. | 35 |
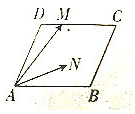 如图,在平行四边形ABCD中,AB=4,AD=2,∠DAB=60°,点M在线段DC上,且满足$\overrightarrow{DM}$=$\frac{1}{4}$$\overrightarrow{DC}$,若N是平行四边形ABCD内的任意一点(含边界),则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是[0,13].
如图,在平行四边形ABCD中,AB=4,AD=2,∠DAB=60°,点M在线段DC上,且满足$\overrightarrow{DM}$=$\frac{1}{4}$$\overrightarrow{DC}$,若N是平行四边形ABCD内的任意一点(含边界),则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是[0,13].