题目内容
3.在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.(1)求数列{an},{bn}的通项公式;
(2)求数列{an(bn-1)}的前n项和为Sn.
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)利用错位相减法、等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d≠0,∵a1,a2,a5依次成等比数列.
∴${a}_{2}^{2}$=a1a5即(1+d)2=1×(1+4d),d≠0,解得d=2.
∴an=1+2(n-1)=2n-1.
数列{bn}满足bn+1=2bn-1,且b1=3.
变形为:bn+1-1=2(bn-1),
∴数列{bn-1}是等比数列,首项与公比都为2.
bn-1=2n,可得bn=2n+1.
∴an=2n-1,${b_n}={2^n}+1$.
(2)an(bn-1)=(2n-1)•2n.
数列{an(bn-1)}的前n项和为Sn=2+3×22+5×23+…+(2n-1)•2n.
2Sn=22+3×23+…+(2n-3)•2n+(2n-1)•2n+1.
∴-Sn=2+2(22+32+…+2n)-(2n-1)•2n+1=-2+2×$\frac{2({2}^{n}-1)}{2-1}$-(2n-1)•2n+1.
可得:${S_n}=(2n-3)•{2^{n+1}}+6$.
点评 本题考查了错位相减法、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
13.已知$|{\overrightarrow a}|=3$,$|{\overrightarrow b}|=8$,$\overrightarrow a•\overrightarrow b=-12$,则$\overrightarrow a与\overrightarrow b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
11.已知命题p:?x∈(2,+∞),2x>x2;命题q:函数f(x)=sin2x+$\sqrt{3}$cos2x的一条对称轴是x=$\frac{7π}{12}$,则下列命题中为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
18.给出下列四个结论,其中一定正确的是( )
| A. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}$ | B. | $\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{BD}$ | C. | $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ | D. | $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{BD}$ |
7.已知椭圆mx2+ny2=1(n>m>0)的离心率为$\frac{{\sqrt{2}}}{2}$,则双曲线mx2-ny2=1的离心率为( )
| A. | 2 | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
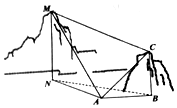 如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的仰角∠MAN=75°,从A点测得C点的仰角∠CAB=30°以及∠MAC=75°,从C点测得∠MCA=60°.已知山高BC=80m,则山高MN=$120+40\sqrt{3}$(m).
如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的仰角∠MAN=75°,从A点测得C点的仰角∠CAB=30°以及∠MAC=75°,从C点测得∠MCA=60°.已知山高BC=80m,则山高MN=$120+40\sqrt{3}$(m).