题目内容
12.已知双曲线的方程为$\frac{x^2}{25}-\frac{y^2}{25}$=1,则此双曲线的离心率为$\sqrt{2}$渐近线方程为y=±x.分析 直接利用双曲线的方程求解双曲线的几何量,推出离心率以及渐近线方程即可.
解答 解:双曲线的方程为$\frac{x^2}{25}-\frac{y^2}{25}$=1,a=5,b=5,c=$\sqrt{2}$,
可得e=$\sqrt{2}$,双曲线的渐近线方程为:y=±x.
故答案为:$\sqrt{2}$;y=±x.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
20.下列推理中属于归纳推理且结论正确的是( )
| A. | 由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n | |
| B. | 由f(x)=xcosx满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数 | |
| C. | 由圆x2+y2=r2的面积S=πr2,推断:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的面积S=πab | |
| D. | 由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2 |
7.已知椭圆mx2+ny2=1(n>m>0)的离心率为$\frac{{\sqrt{2}}}{2}$,则双曲线mx2-ny2=1的离心率为( )
| A. | 2 | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
17.函数y=3x-4x3(x∈[0,2])的最大值是( )
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
2.底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为( )
| A. | $\frac{2\sqrt{2}π}{3}$ | B. | $\frac{\sqrt{2}π}{3}$ | C. | $\frac{2\sqrt{3}π}{3}$ | D. | $\frac{\sqrt{3}π}{3}$ |
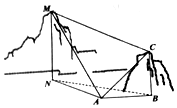 如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的仰角∠MAN=75°,从A点测得C点的仰角∠CAB=30°以及∠MAC=75°,从C点测得∠MCA=60°.已知山高BC=80m,则山高MN=$120+40\sqrt{3}$(m).
如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的仰角∠MAN=75°,从A点测得C点的仰角∠CAB=30°以及∠MAC=75°,从C点测得∠MCA=60°.已知山高BC=80m,则山高MN=$120+40\sqrt{3}$(m).