题目内容
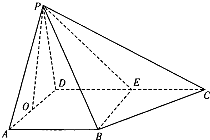 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量| DE |
| AB |
(Ⅰ)求证:平面PAD⊥平面PCD;
(Ⅱ)若PO=
| 3 |
| 2 |
| 7 |
| 21 |
考点:用空间向量求平面间的夹角,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由PO⊥AD,得PO⊥平面ABCD,从而PO⊥DE,由已知得四边形ABED为正方形,从而DE⊥AD,由此能证明平面PAD⊥平面PCD.
(Ⅱ)以O为原点,射线OA所在直线为x轴,过点O作AD的垂线为y轴,建立空间直线角坐标系,利用向量法能求出
平面PAD与平面PBC所成二面角的余弦值.
(Ⅱ)以O为原点,射线OA所在直线为x轴,过点O作AD的垂线为y轴,建立空间直线角坐标系,利用向量法能求出
平面PAD与平面PBC所成二面角的余弦值.
解答:
(Ⅰ)证明:∵PA=PD,O为AD的中点,∴PO⊥AD,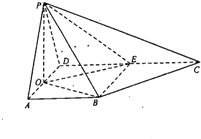
又∵AB⊥PO,AB∩AD=A,∴PO⊥平面ABCD,
又DE?平面ABCD,∴PO⊥DE,
连接OB,OE,则PO⊥OB,PO⊥OE,
又∵AB⊥AD,
=
,AD=AB=2,
∴四边形ABED为正方形,
∴DE⊥AD,又AD∩PO=O,
∴DE⊥平面PAD,又DE?平面PCD,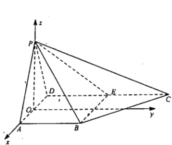
∴平面PAD⊥平面PCD.
(Ⅱ)解:∵PA=PD,O为AD中点,∴PO⊥AD,
又∵AB⊥PO,AB∩AD=A,∴PO⊥平面ABCD,
由(Ⅰ)知AB⊥平面PAD,
∴以O为原点,射线OA所在直线为x轴,过点O作AD的垂线为y轴,
建立空间直线角坐标系,
由条条件得A(1,0,0),B(1,2,0),P(0,0,
),D(-1,0,0),
∵
=
,∴E(-1,2,0),设C(-1,y,0),y>0,
则
=(1,0,-
),
=(-1,0,-
),
=(1,2,-
),
=(-2,0,0),
=(-1,y,-
),
设平面PBE的法向量为
=(x,y,z),由
•
=0,且
•
=0,
得
=(0,
,2),
∴点C到平面PBE的距离为d=
=
=
,
解得y=7(取正值),∴
=(-1,4,-
),
设平面PBC的法向量
=(x,y,z),则由
•
=0,且
•
=0,
得
=(
z,
z,z),取z=
,得
=(1,1,
),
∵
=(0,2,0)\为平面PAD的一个法向量,
∴cos<
,
>=
=
=
.
∴平面PAD与平面PBC所成二面角的余弦值为
.

又∵AB⊥PO,AB∩AD=A,∴PO⊥平面ABCD,
又DE?平面ABCD,∴PO⊥DE,
连接OB,OE,则PO⊥OB,PO⊥OE,
又∵AB⊥AD,
| DE |
| AB |
∴四边形ABED为正方形,
∴DE⊥AD,又AD∩PO=O,
∴DE⊥平面PAD,又DE?平面PCD,

∴平面PAD⊥平面PCD.
(Ⅱ)解:∵PA=PD,O为AD中点,∴PO⊥AD,
又∵AB⊥PO,AB∩AD=A,∴PO⊥平面ABCD,
由(Ⅰ)知AB⊥平面PAD,
∴以O为原点,射线OA所在直线为x轴,过点O作AD的垂线为y轴,
建立空间直线角坐标系,
由条条件得A(1,0,0),B(1,2,0),P(0,0,
| 3 |
∵
| DE |
| AB |
则
| PA |
| 3 |
| PD |
| 3 |
| PB |
| 3 |
| BE |
| PC |
| 3 |
设平面PBE的法向量为
| n |
| n |
| PB |
| n |
| BE |
得
| n |
| 3 |
∴点C到平面PBE的距离为d=
|
| ||||
|
|
|
| ||||
|
| 2 |
| 7 |
| 21 |
解得y=7(取正值),∴
| PC |
| 3 |
设平面PBC的法向量
| m |
| m |
| PB |
| m |
| PC |
得
| m |
| ||
| 3 |
| ||
| 3 |
| 3 |
| m |
| 3 |
∵
| AB |
∴cos<
| AB |
| m |
| ||||
|
|
| 2 | ||
|
| ||
| 5 |
∴平面PAD与平面PBC所成二面角的余弦值为
| ||
| 5 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止,设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是( )



 2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为
2013年12月26日上午,日本首相安倍晋三参拜了靖国神社.这是安倍两次出任首相以来首次参拜,引起周边国家的强烈谴责,我军为了加强防范外敌入侵加强军事演习.在某次军事演习中红方为了准确分析战场形势,在两个相距为 如图,斜三棱柱ABC-A1B1C1的所有棱长都为2,侧面AA1BB1⊥底面ABC,D为CC1中点,E为A1B1的中点,∠ABB1=60°.
如图,斜三棱柱ABC-A1B1C1的所有棱长都为2,侧面AA1BB1⊥底面ABC,D为CC1中点,E为A1B1的中点,∠ABB1=60°. 如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)
如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)