题目内容
 如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)
如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米.已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米.(注:制箱材料必须用完)(1)求出a,b满足的关系式;
(2)问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?
考点:函数模型的选择与应用,棱柱、棱锥、棱台的体积
专题:应用题,不等式的解法及应用
分析:(1)根据流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米,求出a,b满足的关系式;
(2)先将实际问题转化成数学中的函数的最值问题,再利用基本不等式求.
(2)先将实际问题转化成数学中的函数的最值问题,再利用基本不等式求.
解答:
解:(1)由题意可得
,即
------------------------(6分)
(2)因为该杂质的质量分数与a,b的乘积ab成反比,所以当ab最大时,该杂质的质量分数最小
由均值不等式得a+2b≥2
(当且仅当a=2b时取等号)
所以a+2b+ab≥ab+2
,
即ab+2
≤30(当且仅当a=2b时取等号)---------(8分)
即(
+5
)(
-3
)≤0,
因为
>0,所以
≤3
,所以ab≤18-------------(10分)
所以当且仅当
即
时,ab取得最大值18,此时该杂质的质量分数最小---------(12分)
|
|
(2)因为该杂质的质量分数与a,b的乘积ab成反比,所以当ab最大时,该杂质的质量分数最小
由均值不等式得a+2b≥2
| a•2b |
所以a+2b+ab≥ab+2
| 2ab |
即ab+2
| 2ab |
即(
| ab |
| 2 |
| ab |
| 2 |
因为
| ab |
| ab |
| 2 |
所以当且仅当
|
|
点评:此题考查了基本不等式的应用,考查了利用函数知识求解实际问题的知识,解题的关键是理解题意,根据题意构建函数关系,利用基本不等式的知识求最值.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
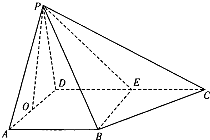 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量