题目内容
从椭圆C:
+
=1(a>b>0)上一点P向X轴作垂线,垂足恰为左焦点F1.A,B分别是椭圆的右顶点和上顶点,且OP∥AB,|F1A|=
+
.
(1)求椭圆C的方程;
(2)已知圆O:x2+y2=2的切线l与椭圆C相交于A,B两点,问以AB为直径的圆是否经过定点?若是,求出定点的坐标;否则,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 3 |
(1)求椭圆C的方程;
(2)已知圆O:x2+y2=2的切线l与椭圆C相交于A,B两点,问以AB为直径的圆是否经过定点?若是,求出定点的坐标;否则,说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)x=c代入椭圆方程求得y,进而求得|PF|,根据OP∥AB,PF∥OB推断出△PFO∽△ABO,根据相似三角形的性质求得b和c的关系,可得a和c的关系,结合a+c=
+
,即可求椭圆C的方程;
(2)先求得直线l的斜率不存在及斜率为0时圆的方程,由此可得两圆所过公共点为原点O,当直线l的斜率存在且不为零时,设直线l的方程为y=kx+m,代入椭圆方程消掉y得x的二次方程,设A(x1,y1),B(x2,y2),由韦达定理、向量数量积可得
•
的表达式,再根据线圆相切可得k,m的关系式,代入上述表达式可求得
•
=0,由此可得结论
| 6 |
| 3 |
(2)先求得直线l的斜率不存在及斜率为0时圆的方程,由此可得两圆所过公共点为原点O,当直线l的斜率存在且不为零时,设直线l的方程为y=kx+m,代入椭圆方程消掉y得x的二次方程,设A(x1,y1),B(x2,y2),由韦达定理、向量数量积可得
| OA |
| OB |
| OA |
| OB |
解答:
解:(1)由已知,|F1A|=
+
,
∴a+c=
+
,
把x=c代入椭圆方程求得y=±
,
∴|PF|=
,
∵OP∥AB,PF∥OB
∴△PFO∽△ABO
∴
=
,
求得b=c
∴a=
,b=
∴椭圆C的方程为
+
=1; …(5分)
(2)当切线与x轴垂直时,l:x=±
,
椭圆中,令l:x=±
,得y=±
,
∴以AB为直径的圆的方程为(x±
)2+y2=2,两圆唯一的公共点为(0,0);…(8分)
当切线与x轴不垂直时,可设切线的方程为;y=kx+m
联立方程x2+2y2=6,得(1+2k2)x2+4kmx+2(m2-3)=0
由直线与圆相切得,
=
,即m2=2(1+k2)…(10分)
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
∵m2=2(1+k2),∴m2-2k2-2=0,∴
•
=0
即以AB为直径的圆过(0,0).
综上得,以AB直径的圆经过定点(0,0).…(14分)
| 6 |
| 3 |
∴a+c=
| 6 |
| 3 |
把x=c代入椭圆方程求得y=±
| b2 |
| a |
∴|PF|=
| b2 |
| a |
∵OP∥AB,PF∥OB
∴△PFO∽△ABO
∴
| b2 | ||
|
| b |
| a |
求得b=c
∴a=
| 6 |
| 3 |
∴椭圆C的方程为
| x2 |
| 6 |
| y2 |
| 3 |
(2)当切线与x轴垂直时,l:x=±
| 2 |
椭圆中,令l:x=±
| 2 |
| 2 |
∴以AB为直径的圆的方程为(x±
| 2 |
当切线与x轴不垂直时,可设切线的方程为;y=kx+m
联立方程x2+2y2=6,得(1+2k2)x2+4kmx+2(m2-3)=0
由直线与圆相切得,
| |m| | ||
|
| 2 |
设A(x1,y1),B(x2,y2),则x1+x2=
| -4km |
| 1+2k2 |
| 2(m2-3) |
| 1+2k2 |
|
∵m2=2(1+k2),∴m2-2k2-2=0,∴
| OA |
| OB |
即以AB为直径的圆过(0,0).
综上得,以AB直径的圆经过定点(0,0).…(14分)
点评:本题考查椭圆的方程、圆的方程及直线与椭圆的位置关系,考查向量的数量积运算,考查学生解决问题的能力.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
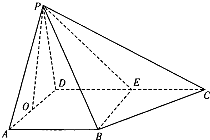 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量