题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,右焦点为(
,0).
(1)求椭圆C的方程;
(2)过原点O作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值;
(3)在(2)的条件下,求△OAB面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 2 |
(1)求椭圆C的方程;
(2)过原点O作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值;
(3)在(2)的条件下,求△OAB面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆C的方程.
(2)设A(x1,y1),B(x2,y2),设直线AB:y=kx+m.由
,得(1+3k2)x2+6kmx+3m2-3=0,由此利用根的判别式、韦达定理、点到直线AB的距离公式,能证明点O到直线AB的距离为定值
.
(3)|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
)2-4×
]≤4,当斜率不存在时,|AB|<2.由此能求出△OAB面积的最大值.
|
(2)设A(x1,y1),B(x2,y2),设直线AB:y=kx+m.由
|
| ||
| 2 |
(3)|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)的离心率为
,右焦点为(
,0),
∴
,解得a=
,b=1,
∴椭圆C的方程
+y2=1…(3分)
(2)证明:设A(x1,y1),B(x2,y2),若k存在,则设直线AB:y=kx+m.
由
,得(1+3k2)x2+6kmx+3m2-3=0…(5分)
△>0,
…(6分)
有OA⊥OB,知x1x2+y1y2=x1x2+(k x1+m)(k x2+m)
=(1+k2) x1x2+k m(x1+x2)+m2=0,…(8分)
代入,得4m2=3k2+3,原点到直线AB的距离d=
=
.…(9分)
当AB的斜率不存在时,|x1|=|y1|,
可得|x1|=
=d,依然成立.
∴点O到直线AB的距离为定值
…(10分)
说明:直接设直线OA的斜率为K相应给分
(3)|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
)2-4×
]
=
=3+
=3+
≤4 …(12分)
当且仅当9k2=
,即k=±
时等号成立.…(13分)
当斜率不存在时,经检验|AB|<2.
∴S△OAB≤
×2×
=
综合得:△OAB面积的最大值为
.…(14分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 2 |
∴
|
| 3 |
∴椭圆C的方程
| x2 |
| 3 |
(2)证明:设A(x1,y1),B(x2,y2),若k存在,则设直线AB:y=kx+m.
由
|
△>0,
|
有OA⊥OB,知x1x2+y1y2=x1x2+(k x1+m)(k x2+m)
=(1+k2) x1x2+k m(x1+x2)+m2=0,…(8分)
代入,得4m2=3k2+3,原点到直线AB的距离d=
| |m| | ||
|
| ||
| 2 |
当AB的斜率不存在时,|x1|=|y1|,
可得|x1|=
| ||
| 2 |
∴点O到直线AB的距离为定值
| ||
| 2 |
说明:直接设直线OA的斜率为K相应给分
(3)|AB|2=(1+k2)(x1-x2)2=(1+k2)[(
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
=
| 3(9k4+10k2+1) |
| 9k4+6k2+1 |
| 12k2 |
| 9k4+6k2+1 |
| 12 | ||
9k2+6+
|
当且仅当9k2=
| 1 |
| k2 |
| ||
| 3 |
当斜率不存在时,经检验|AB|<2.
∴S△OAB≤
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
综合得:△OAB面积的最大值为
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查点到直线的距离为定值的证明,考查三角形面积的最大值的求法,解题时要认真审题,注意点到直线的距离公式和弦长公式的合理运用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
若P(2,-1)为圆
(θ为参数且0≤θ<2π)的弦的中点,则该弦所在的直线方程为( )
|
| A、x-y-3=0 |
| B、x+2y=5 |
| C、x+y-1=0 |
| D、2x-y-5=0 |





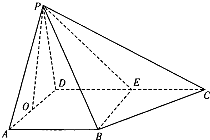 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量