题目内容
已知函数f(x)=2f′(1)lnx+x2+2f(1)x+
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=f(x)-x2+(
-a)x-
-
,证明:当a≥1时.对任意的x∈[0,1),g(1-x)≤g(1+x).
| 1 |
| 4 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=f(x)-x2+(
| 5 |
| 2 |
| a-1 |
| x |
| 1 |
| 4 |
考点:利用导数求闭区间上函数的最值,导数的运算
专题:导数的综合应用
分析:(Ⅰ)根据f(x)的解析式可求出f(1),f′(1),从而求出f(x);
(Ⅱ)求出g(x),令p(x)=g(1+x)-g(1-x),因为p(0)=0,所以想法证明p(x)在[0,1)上是增函数,这样便能得到p(x)≥p(0)=0,所以g(1+x)≥g(1-x),所以g(1-x)≤g(1+x).所以通过求p′(x),并说明p′(x)≥0,从而证出p(x)是增函数,即证出g(1-x)≤g(1+x).
(Ⅱ)求出g(x),令p(x)=g(1+x)-g(1-x),因为p(0)=0,所以想法证明p(x)在[0,1)上是增函数,这样便能得到p(x)≥p(0)=0,所以g(1+x)≥g(1-x),所以g(1-x)≤g(1+x).所以通过求p′(x),并说明p′(x)≥0,从而证出p(x)是增函数,即证出g(1-x)≤g(1+x).
解答:
解:(Ⅰ)f(1)=1+2f(1)+
,∴f(1)=-
;
f′(x)=
+2x-
,∴f′(1)=2f′(1)+2-
,∴f′(1)=
;
∴f(x)=lnx+x2-
x+
;
(Ⅱ)g(x)=lnx-ax-
;
令p(x)=g(1+x)-g(1-x),则:
p(x)=ln(1+x)-a(1+x)-
-[ln(1-x)-a(1-x)-
]=ln(1+x)-ln(1-x)-2ax-(a-1)[
-
],∴p′(x)=
+
-2a+(a-1)[
+
]=
-2a+(a-1)[
+
]
下面证明p′(x)≥0,即证:
-2a+(a-1)[
+
]≥0;
即证:
-a+(a-1)[
]≥0;
∵x∈[0,1),由
≥1,即证1-a+(a-1)[
]≥0;
又a-1≥0,只需证-1+
≥0;
即证1+x2≥(1+x)2(1-x)2,即证x4-3x2≤0;
∵x∈[0,1),∴x2(x2-3)≤0成立,∴x4-3x2≤0成立;
即p(x)在[0,1)上单调递增,∴p(x)min=p(0)=0;
∴p(x)≥0,g(1+x)≥g(1-x),∴g(1-x)≤g(1+x).
| 1 |
| 4 |
| 5 |
| 4 |
f′(x)=
| 2f′(1) |
| x |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∴f(x)=lnx+x2-
| 5 |
| 2 |
| 1 |
| 4 |
(Ⅱ)g(x)=lnx-ax-
| a-1 |
| x |
令p(x)=g(1+x)-g(1-x),则:
p(x)=ln(1+x)-a(1+x)-
| a-1 |
| 1+x |
| a-1 |
| 1-x |
| 1 |
| 1+x |
| 1 |
| 1-x |
| 1 |
| 1+x |
| 1 |
| 1-x |
| 1 |
| (1+x)2 |
| 1 |
| (1-x)2 |
| 2 |
| 1-x2 |
| 1 |
| (1+x)2 |
| 1 |
| (1-x)2 |
下面证明p′(x)≥0,即证:
| 2 |
| 1-x2 |
| 1 |
| (1+x)2 |
| 1 |
| (1-x)2 |
即证:
| 1 |
| 1-x2 |
| 1+x2 |
| (1+x)2(1-x)2 |
∵x∈[0,1),由
| 1 |
| 1-x2 |
| 1+x2 |
| (1+x)2(1-x)2 |
又a-1≥0,只需证-1+
| 1+x2 |
| (1+x)2(1-x)2 |
即证1+x2≥(1+x)2(1-x)2,即证x4-3x2≤0;
∵x∈[0,1),∴x2(x2-3)≤0成立,∴x4-3x2≤0成立;
即p(x)在[0,1)上单调递增,∴p(x)min=p(0)=0;
∴p(x)≥0,g(1+x)≥g(1-x),∴g(1-x)≤g(1+x).
点评:本题考查求函数解析式,构造函数的方法,通过判断函数导数符号判断函数单调性的方法,函数的最小值,分析法证明问题的方法.

练习册系列答案
相关题目




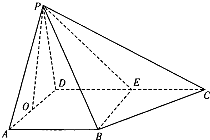 如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量
如图,在四棱锥P-ABCD中,已知AB⊥AD,PA=PD,D为AD的中点,AB⊥PO,E为线段DC上一点,向量